On the density of doubles and floats

With finite precision numbers, if you take a small number eps, there comes a point when x == x + eps. Here's some code that figures out when that happens:

double epsD(double x) {
    double r;
    r = 1000.0;
    while ( x < (x + r) )
        r = r / 2.0;
    return ( 2.0 * r );
}

With x around one the resolution limit is roughly at 1e-16 for doubles, and 1e-7 for floats. The top data points show how the relative accuracy stays constant, so at x=1e7 the resolution is only about eps=1 for floats.

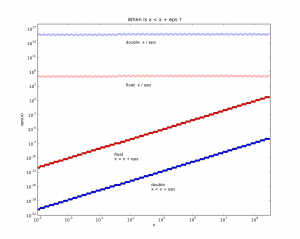
Thinking about CAD/CAM related stuff, if you have a fancy top of the line CNC-machine with the longest axis x=1000mm and a theoretical accuracy of one micron, or 0.001mm, then we're at the point where we really should use doubles (which are slower, but how much slower?).

python source for plotting the figure: epsplot.py.tar