Category: CNC

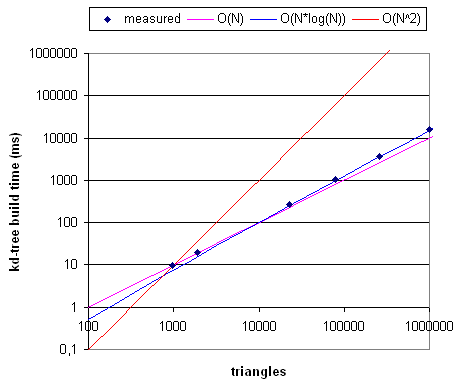
Timing build_kdtree()

Drop-cutter requires a fast way of searching for triangles under the tool. A kd-tree (4-dimensional in this case) is suggested by Yau et al. I've tried to implement one here (look in trunk/Project2). Just ran some timing tests using Stopwatch() on it, and indeed the build_kdtree() function which takes a pile of triangles as input and generates a kd-tree seems to run in O(N*log(N)) time as it should.

I've never drawn this type of plot before, and I was surprised at how close N*log(N) is to N - in a loglog plot they are almost equal!

This is a recursive function. I wonder if there's a good way of multi-threading recursive functions? My laptop is dual-core and a modern desktop PCs is likely a quad-core - so let's try to write these things multi-threaded from the start.

Next up is a function for doing the orthogonal range-search for triangles that lie under the tool. That's supposed to run in O(N^(1-1/D)+K) time, where D is the dimension of the tree and K is the number of reported triangles - so O(N^(3/4)+K) in this case. I'll try to get that done during the weekend.

E-stop circuit

This is the E-stop circuit I am going to use when upgrading the cnc-mill to servo control. The idea is to use a wire-OR circuit (series connection of NC switches) for things that cause an E-stop followed by a wire-AND circuit (parallel connection of relays) for things I want to happen at E-stop.

The E-stop out signal from EMC is wired to the top right of this board (labeled E-stop IN...). When this signal goes high it closes the rightmost relay which has +12V wired to it. The 12 V then goes through a series of NC switches, which I've here just shorted out with the black wires. In reality the black wires will be replaced by one E-stop button on the main enclosure, one E-stop button on the jog-pendant, X/Y/Z limit switches, NC servo-amp fault relays, and a VFD NC fault relay.

When all is well +12 V is supplied to the three other relays, and these provide NC or NO outputs. One is used to tell EMC everything is OK (E-stop IN signal in EMC), one is used to enable the power switch of the axis servos, and one is spare for now.

This should make the machine reasonably safe. If any of the E-stop buttons are pressed, a limit is tripped, or the servo amps/VFD are not feeling well we should go into E-stop, and that will cut power from the servos. EMC will also notice this and I'm relying on EMC to shut down the coolant pump and the VFD.

Z-map model for 3-axis machining

I've been reading about the z-map model for 3-axis milling. A working simulation environment would be very useful for CAM algorithm development. Coarse errors in the algorithms can be spotted by eye from the simulation, and a comparison of the z-map with the original CAD model can be used to see if the machining really produces the desired part within tolerance.

Jeff Epler hacked together a z-map model with EMC2 a while ago: gdepth. Perhaps some code/ideas can be borrowed from there.

The z-map can also be used for generating the tool paths themselves (similar to bitmap-mowing here, here and here), but that's more advanced and not the immediate goal.

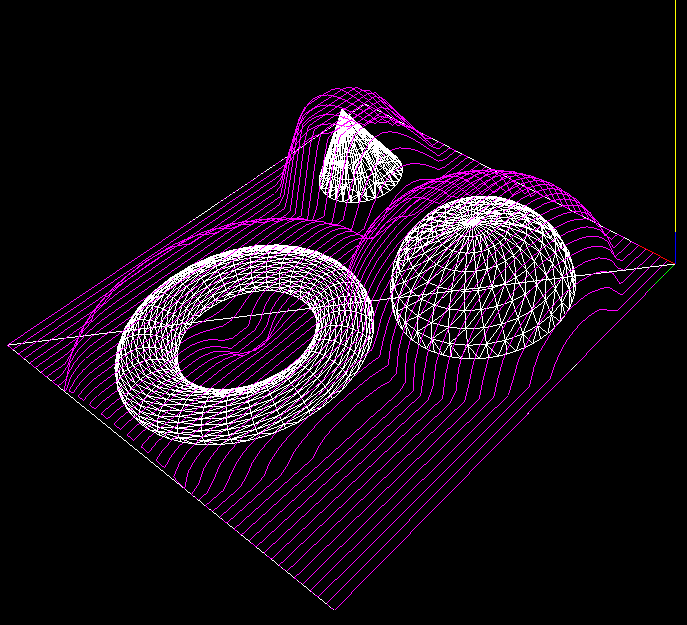
Here's the z-map model, a lot of vectors standing upright in the z-direction, getting cut (or mowed down) by the moving tool. For graphics you could fill each space between four z-vectors with two triangles and display an STL surface. Obviously this works only for 3-axis machining where the tool is oriented along the z-axis, and the tool must also not produce undercuts (e.g. T-slot milling).

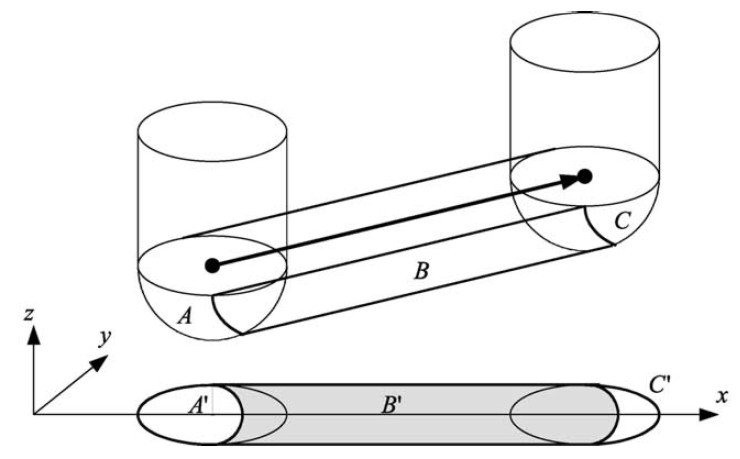
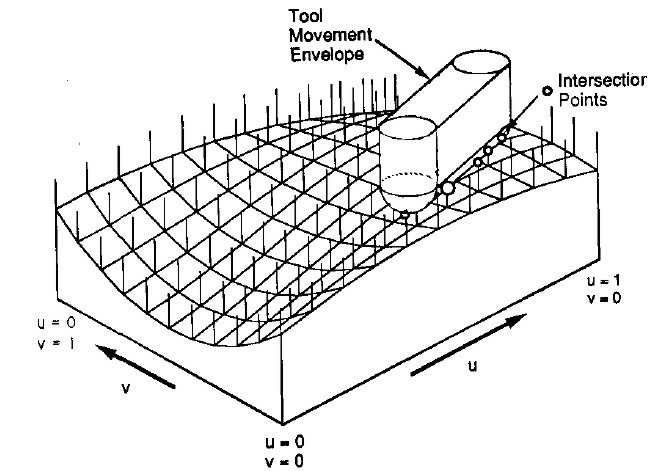
So how do you cut down the z-vectors for each move in the program? For linear moves you can always rotate your coordinate system so it looks like the figure above. The movement is along the x axis, with possibly a simultaneous move in the z-axis. At the beginning of each move (A) and at the end (C) it's very simple, you just calculate the intersection of the relevant z-vectors with a stationary tool at A and C, a kind of 'inverse drop-cutter' idea.

The surface the tool sweeps out during the move itself (B) is more difficult to deal with. The mathematics of the swept surface leads to an equation which most people seem to solve numerically by iteration. I'd like to go through the math/code in a later post (need to learn how to put equations in posts first!).

It's not smart to test all z-vectors in the model against the tool envelope of each move. So like drop-cutter where you are searching for which triangles are under the tool, in z-map you want to know which z-vectors are under the tool envelope. One strategy is simple bucketing, but perhaps if a kd-tree is developed for drop-cutter the same algorithm can be used for z-map.

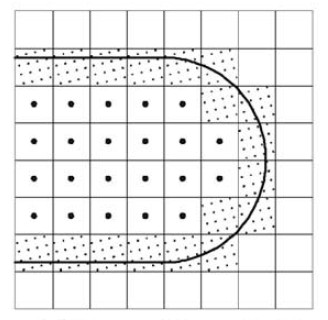
Obviously the z-map has a finite resolution. Increasing the linear resolution by some factor a requires a^2 more z-vectors, storage, and calculations. A better way might be to insert more z-vectors only where they are needed. That's the places on the model where the z-coordinate changes a lot. So here (view from above) for example if you are milling with a cylindrical cutter more z-vectors are needed along the edge of the tool envelope. (I have no idea why they are inserted in a tilted grid-pattern in the above figure...). This potentially leads to much reduced memory/calculation requirements, while still producing a high resolution model. As the simulation progresses there are probably also regions where some densely spaced z-vectors could be removed. Maybe a 'garbage-collector' process could go over the model every now and then and look for flat areas (xy-plane like regions) where less z-vectors are needed and remove them.

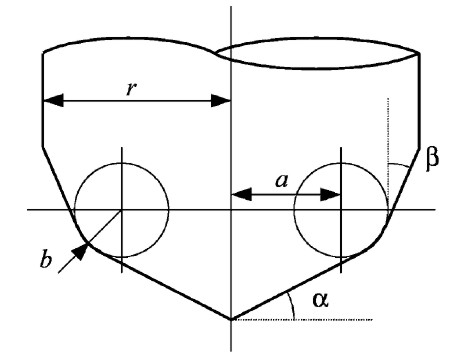
A lot of papers use this APT tool when deriving the equations for machining or simulations. By varying the parameters suitably you get the familiar tool shapes below:

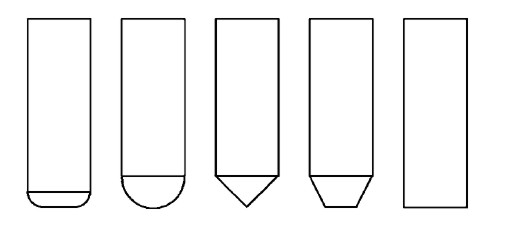
From left to right: Bull-nose/filleted/toroidal, Round/ball-nose/spherical, drill/countersink, tapered, and cylindrical.

My earlier drop-cutter explanations and code only work with the toroidal, spherical, and cylindrical cutters. I'm not sure if it makes sense to write the code for the general APT cutter, or if it's better to optimize for each case (cylindrical and spherical are usually quite easy).

If anyone has made it this far, my sources are the following papers - which are available from me if you ask nicely by email.

Mowing Foam

Dan Egnor sent me this nice example of bitmap-based toolpath generation, or 'pixel mowing'. It's a slightly exaggerated topographic relief of San Francisco machined in tooling board using a very simple 'lawn mowing' toolpath generator.

The explanation of how it works below is mostly Dan's, not mine.

This is the input to the toolpath generator for one of the Z-slices.

black - material which must not be touched
green - to be removed, is safe (at least one tool radius from black)
yellow - remove if possible, is dangerous (within tool radius of black)
purple - has been cleared, is dangerous (machine limits or similar)
white - has been cleared, is safe, is not blue (below)
blue - this spot has been cleared, and is safe, but is within one tool radius of material that needs clearing (green or yellow)

Note that you don't see blue in either "before" or "after" images, it only occurs transiently. (In theory it could show up in "before" as area outside the workpiece.)

And this is the resulting toolpath. Green circles are plunges and red circles are lifts. The thick grey lines represent actual cuts, the thinner lines are rapid feeds.

The basic rule is that the tool *centroid* is only allowed to visit safe areas (green, blue, and white). Green and blue represent work to be done (safe areas that need visiting). Of course, as the tool moves, green changes to blue and white, and (some) yellow changes to purple.

The real trick is in efficiently tracking the "within tool radius of" zones (material to be cut, or material to stay away from). Every pixel keeps a count of how many pixels of each type ("nearby-blocking" or "nearby-cutting") are within one tool radius of that pixel. Whenever a value is changed ( e.g. the simulated tool moves and changes some points from "cut" to "clear"), every counter within the appropriate radius is updated.

That would be rather costly to implement directly, each simulated pixel move would require N^3 updates, if N is the diameter of the tool. Instead those counters are only kept as *differences* between each point and its neighbours. That means changing a point only requires updating the values along the *perimeter* of the radius surrounding that point, meaning that a simulated pixel move only requires N^2 updates, which makes things a lot more tractable (though it still takes the old laptop I use a couple minutes to complete the toolpaths for a 5" x 3" x 1.5" model at 1/256" resolution). Of course this means that the "color state" isn't directly accessible for a random pixel, but must be figured incrementally from neighboring values. Fortunately most operations don't access random pixels.

You would probably not want to cut metal with this kind of algorithm as there is no control over material removal rate or cutting forces, but for foam, tooling-board, or wood it should work ok.

Dan's program is written in C++ and available here (http://svn.ofb.net/svn/egnor/boring/), but it's not well documented.

We are standing by for a video of this kind of cutting!

Mowing tactics

Moving forward with the CAM coding, the sensible thing would probably be to work on mundane things like 2D offset generation, a kd-tree for faster drop-cutter searches, and zigzag-paths from 2D outlines... There's again been some talk about open-source CAM on cnczone, but not much in terms of results or actual descriptions or implementations of toolpath algorithms.

Anyway, here's something more fun than the traditional computational geometry problems I referred to above. It's lawn-mowing tactics, or how do you program the circular robot to mow the red pixels while not cutting too many of them at a time. This is a slightly improved version of my earlier trial. This one considers a number of angles in all directions for each move. From these moves the ones that cut away a suitable amount of material are selected. Additionally I've introduced a cost function for changing direction, it should be easier for the cutter to continue traveling in approximately the same direction than to do abrupt turns. In spite of this, about half-way through the cutter reverses direction...This is obviously done with a bitmap representing the grass to be mowed, but I wonder if it would be better to try to do it more exactly: represent the boundaries of the grass with lines and arcs. A variable step-length also seems like a good idea, on long straight bits the cutter should be able to move in one go as far as it goes.

Spinning the DC Servos

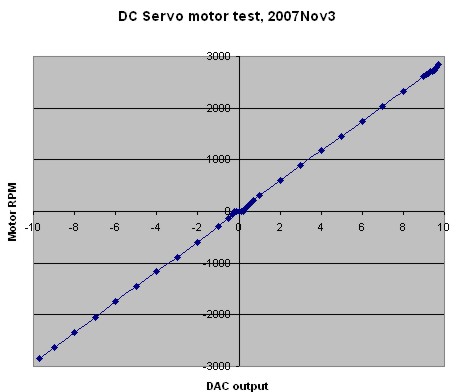
Some good steps towards driving our cnc-mill with DC-servos taken today. I got the pico-systems servodrives wired correctly, the new 50 kHz PWM m5i20 configuration loaded onto the fpga, and updated my pyvcp test panel a bit. I'm using three 19" rack enclosures. The lower one has a 1.8 kVA transformer, the middle one houses the servodrives, and the top one has differential encoder cards for the motors and optoisolator interfaces to the m5i20.

One small setback was that the servodrives wanted the PWM in reverse polarity compared to what I had available. There's nothing in the m5i20 driver to reverse the polarity of the DAC output PWM. Fortunately the drives have optocoupler inputs so instead of GND-PWM I wired them in a PWM-Vcc configuration and it worked OK. I did an open-loop no load test (below) where I monitored the RPM while changing the DAC output. There's a bit of dead-band in the middle where nothing happens between DAC values of about -0.2 and +0.2. After that the curve is pretty linear up to +9.7 after which the PWM pulse becomes unacceptably short for the servodrive and at DAC=9.8 or above the motors just jump and stutter. So eventually with EMC and PID control I need to limit the DAC range to [-9.7 , +9.7].

Next is probably trying out closed-loop PID control, and after that I need to look at the E-stop chain, home switches, a relay for the flood coolant pump, and controlling the VFD/Spindle.

pyVCP m5i20 HOSTMOT-4 test panel

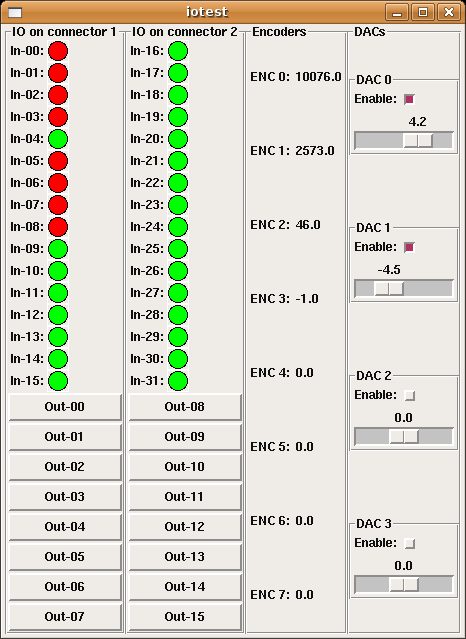
For testing the servo-drives and all the electronics I found this test-panel for the HOSTMOT-4 conifiguration of the m5i20 quite useful.

It uses an XML file (iotest.xml) to define the pyVCP panel layout, and then a HAL file (pyiotest.hal) to hook up the IO pins of the m5i20 to the panel. I'm also using a shell script (iotest.sh) to start the realtime environment and run pyvcp followed by the HAL file automatically.

Compare this to my earler effort with the old VCP. Now with many more widgets in pyVCP I have better control of the DACs etc.

Drop-Cutter in C# - v2

I think I've found the problems with my C# drop-cutter algorithm. The first bug was a trivial one where in the edge-test the rotation of the segment-under-test was messed up. The second one was not the facet-test itself but incorrect surface normal data. There's something going on that makes pre-calculated surface normal data not 'stick' correctly to the triangle object for later use. So here I'm re-calculating the normal data again just before the facet test.

The next step is to speed up things with a smarter kd-tree based search for which triangles are under the cutter. I've added bounding-boxes to the Cutter and Triangle classes. Running the above example the DropCutter function is called a total of 4735000 times, and of those only less than 5%, or 236539 to be exact, are useful calls, i.e. the triangle bounding box intersects the cutter bounding box, which means there's a chance that we are contacting the cutter against the triangle. The idea with the kd-tree then is to pre-search for triangles under the cutter to make less of those (supposedly expensive) redundant calls to DropCutter.

On my T5600 processor machine the above example runs in about 5 seconds. (1894 triangles, about 4.7 Million calls to DropCutter of which ca 240k calculate something). I've made a list of useful CAM-related things to work on: CAMToDo.