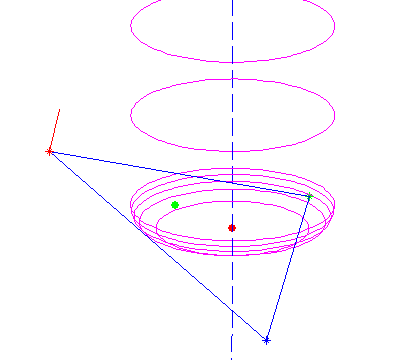
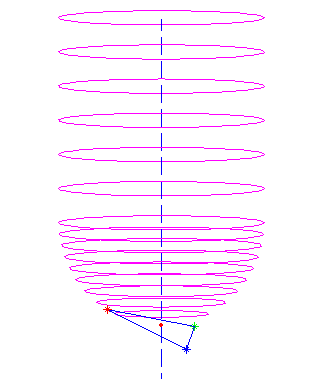
The facet test I wrote about yesterday needs a 'point in triangle' test to determine if the found CC point lies within the given triangle and we should thus care about the ze value the algorithm determined, or if the CC point is outside, and we can skip to the next test/triangle.
I wrote a function isright(p1,p2,p) which tells me whether the point p is right or left of the line from p1 to p2. The triangle test isinside(p1,p2,p3,p) uses this function three times:
t1 = isright(p1,p2,p);
t2 = isright(p3,p1,p);
t3 = isright(p2,p3,p);
and if t1, t2, t3 all have the same sign then p is inside the triangle.
If I add this function to the facet test, I can determine which of the CC points in the plane containing the triangle are within the triangle:
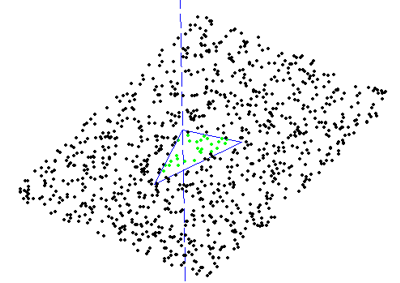
here the dashed line indicates the z-axis.
I'm a little concerned that this works with the projection of the triangle onto the xy-plane. But maybe that isn't a problem because triangles with horizontal normals are special cases anyway. I also haven't yet looked at the rounding/on-edge problems Julian talks about.
I wish the third and final part of this story, the edge-test, was as simple as the vertex and facet tests! At least so far I haven't found a really simple algorithm for the edge-test in the literature (I'm reading Hwang1998 and Chuang2002). Anyone know more about this? please comment below!