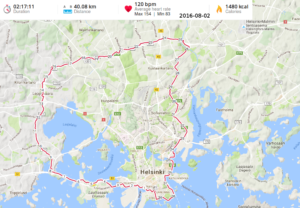
Windy weather and low fitness makes for slow riding...
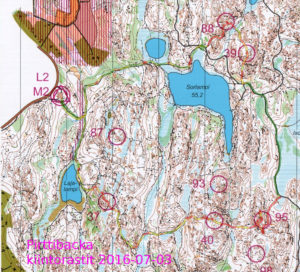
Pirttibacka kiintorastit, south
Tattarisuo racing
Hydrogen
HFO and dissociator of H-maser after replacing the H2-source in one of our H-masers.
See also: the same but different on another maser.
USRP N210 quickstart
For various experiments I got an USRP N210. Here's how to get going with gnuradio.
By default it shows up at 192.168.10.2, so configure your PC eth-interface on 192.168.10.XXX. Now
$ uhd_find_devices
Should find the device:
--------------------------------------------------
-- UHD Device 0
--------------------------------------------------
Device Address:
type: usrp2
addr: 192.168.10.2
However uhd_usrp_probe suggest upgrading the firmware and FPGA image, so we do that by:
$ sudo /usr/lib/uhd/utils/uhd_images_downloader.py
$ sudo /usr/bin/uhd_image_loader --args="type=usrp2,addr=192.168.10.2"
and after power-cycling the device we now get (in addition to a long description of the RX and TX interfaces or installed daughter-boards):
$ uhd_usrp_probe
FW Version: 12.4
FPGA Version: 11.1
To show that it works in gnuradio a simple USRP-source can be connected to a QT GUI Sink (or QT GUI Frequency Sink) that visualizes RX I/Q samples:
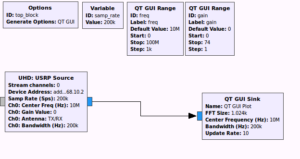
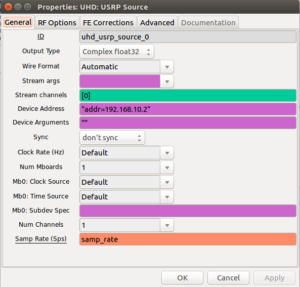
The source needs to be configured with "addr=192.168.10.2" and it uses the samp_rate, freq, and gain variables.
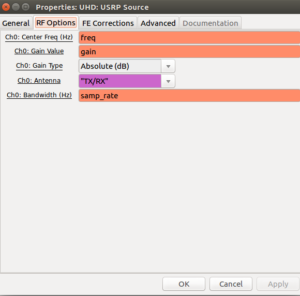
The USRP now samples at 100 MS/s, digitally downconverts a bandwidth samp_rate around a center frequency freq, and streams the samples over Ethernet to the gnuradio source node. When setting freq=10e6 and samp_rate=200k (the minimum possible!?) and applying a 10.020 MHz sine-wave to the RF1-input we get this:
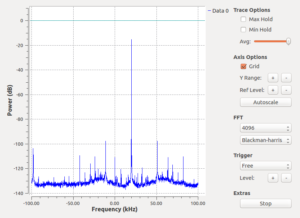
With a signal that seems close to maximum amplitude the dB-scale shows a peak at -16 dB, and without any signal applied the noise-floor close to the center frequency dips just below -140 dB rising to -135 dB at 20 kHz offset.
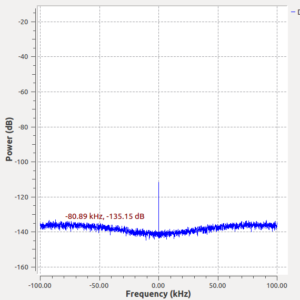
Awesome stuff! The 200 kS/s samples from one I/Q channel produce about 800 kB/s of Ethernet traffic.
Stay tuned for more SDR updates in the near future!
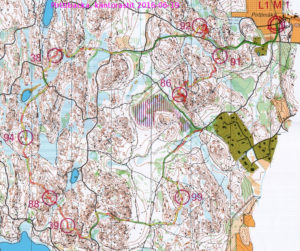
Pirttibacka kiintorastit, north
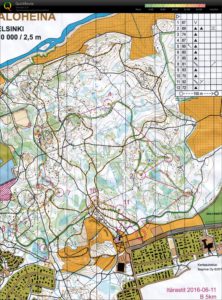
Itärastit Paloheinä
Espoorastit Ämmässuo
After a long walk to the start #1 went OK, a bit far north on #2, fairly safe route to #3. #5-#6 is probably the worst split as the open area was slow and my position was uncertain after the road. #7 was more nicer terrain for a change. At the end drifted too much south at #11 - this is an area that has been difficult before also...
Nice weather with a bit of wind. A lot of people preparing for Jukola in 1.5 weeks.
Länsirastit Oittaa
scipy.stats.chi2.ppf() without scipy
Allantools has a dependence on scipy because it uses scipy.stats.chi2.ppf() (inverse of the chi-squared cumulative distribution function) in the code for confidence intervals.
When testing scipy takes quite a long time to install and the whole package seems a bit overkill for just this one function.
So I tried implementing it using just numpy. It sort of works, but not for corner cases where p is very close to 1.0 or k is a big number. I get for example:
top = pow(x, s)*math.exp(-x)*pow(x,k) OverflowError: (34, 'Numerical result out of range')
Maybe there's something trick when numerically evaluating lower_gamma() using the series expansion that I am missing...
import scipy.stats import math import numpy def bisection(function, k, p, a, b, tol): # http://code.activestate.com/recipes/578417-bisection-method-in-python/ assert (function(a,k)-p)*(function(b,k)-p) < 0 # a, b must bracket root c = (a+b)/2.0 while (b-a)/2.0 > tol: if (function(c, k)-p) == 0: return c elif (function(a,k)-p)*(function(c,k)-p) < 0: b = c else : a = c c = (a+b)/2.0 return c def lower_gamma(s,x): # lower incomplete gamma function # https://en.wikipedia.org/wiki/Incomplete_gamma_function#Evaluation_formulae g = 0 last_g = 1.0 done = False tol = 1.0e-6 k=0 while not done: top = pow(x, s)*math.exp(-x)*pow(x,k) bot = numpy.prod( [float(s+j) for j in range(k+1) ] ) dg = float(top)/float(bot) if dg == float("Inf"): break g += dg k += 1 if k>100: # get at least 100 terms in the sum if g==0: break delta = abs(dg/g) if delta == float("Inf"): break if delta < tol: done = True last_g = g return g def chi2_cdf(x, k): # chi-squared cumulative density function # cdf(x; k) = lower_gamma(k/2, x/2) / gamma(k/2) return lower_gamma(k/2.0, x/2.0) / math.gamma(k/2.0) def chi2_ppf(p, k): # chi-squared Percent point function (inverse of cdf percentiles). # look for x such that # p = chi2_cdf( x=chi2_ppf(p, k), k) tol = 1e-8 lolim = 0 hilim = k while (chi2_cdf(lolim,k)-p)*(chi2_cdf(hilim,k)-p) > 0: hilim *= 1.5 return bisection( chi2_cdf, k, p, lolim, hilim, tol) print "scipy cdf: ",scipy.stats.chi2.cdf(55, 33) print "own cdf: ",chi2_cdf(55, 33) print "scipy ppf ", scipy.stats.chi2.ppf(0.4, 33) print " own ppf ", chi2_ppf(0.4, 33) # test that we really found the inverse print scipy.stats.chi2.cdf(scipy.stats.chi2.ppf(0.4, 33), 33) print chi2_cdf( chi2_ppf(0.4, 33), 33 ) # try to check the scipy function against our own function # for some random input of (p, k) for n in range(100): k = numpy.random.randint(20, 200) p = numpy.random.random() print k, p, a=scipy.stats.chi2.ppf(p, k) b=chi2_ppf(p, k) ok = numpy.isclose(a, b) if ok: print ok else: print ok, a, b assert ok |