Hadamard total deviation in allantools

Following on from modified total deviation mtotdev() the Hadamard total deviation htotdev() algorithm is very similar but instead of phase data takes frequency data. Now included in allantools.

Here's a comarison against Stable32 and the NIST SP 1065 table values.

There's no bias-correction for now, and apparently it is customary not to use htotdev(m=1) at an averaging-factor of 1, but instead use ohdev(m=1). This is why the 'raw' value from allantools at tau=1 in the plot below is a factor of 2 too low.

htotdev_2016-03-27Both mtotdev() and htotdev() are very slow algorithms - help with making them faster would be appreciated!

Sub-second synchronization of cron jobs

cron_syncWe use cron-jobs to control lab instruments once a minute in the lab. I noticed that specifying 'once a minute' to cron produces a start-time for the job with quite a bit of variability. Usually the job starts at 1s past the minute, but sometimes 2s. There's also a random delay of 20 ms to 50 ms (but sometimes up to 300 ms). This probably depends a lot on the hardware. So if we assume the cron-job starts 1s past the minute the worst error I saw in the test above is 1.3 seconds.

Here's a very simple synchronization idea: first ask for a time-stamp, then wait until we are at an inter-second boundary, then continue. This makes the cron-job continue at the inter-second boundary with a maximum error of 6 ms, a fair improvement over 1.3 seconds without any sync code.

import datetime
import time
 
dt1 = datetime.datetime.now() # time-stamp when cron decides to run us
usecs_to_go = 1e6-dt1.microsecond # we want to run at an inter-second boundary
secs_target = 5 # we want to run at 5 seconds past minute
secs_to_go = secs_target - dt1.second -1 # amount of waiting to do.
time.sleep( secs_to_go+ usecs_to_go/1.0e6 )
dt2 = datetime.datetime.now() # now we are synced!?
 
fn = '/home/user/my_cron_log.txt' 
 
# write to logfile for later analysis.
with open(fn,'a+') as f:
    f.write(str(dt1) +" %02d.%06d" % (dt1.second, dt1.microsecond)  + ' run!\n')
    f.write(str(dt2) +" %02d.%06d" % (dt2.second, dt2.microsecond)  + ' sync!\n')
    f.write('\n')

The way to enable this to run from crontab is to add something like this to crontab (use crontab -e):

# m h  dom mon dow   command
  * *  *   *   *     /usr/bin/python /home/user/cron_sync.py

Where cron_sync.py is the name of the script above.

I'd be interested in hearing how this works on other hardware, or if there are some alternative solutions.

Modified Total Deviation in allantools

I wrote a first rough (and very slow!) implementation of Modified Total Deviation mtotdev() for allantools.

mtotdev() combines the features of modified Allan deviation mdev() (being able to distinguish between white and flicker phase modulation) and Total deviation totdev() (better confidence intervals at large tau).

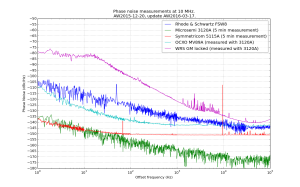
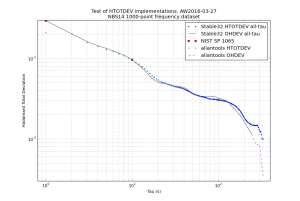
Here are some results. The Time Total Deviation ttotdev() follows trivially from this work also, since it is only a scaled version of mtotdev(). I used the "NBS14" 1000-point frequency dataset and compared my results against Stable32 and those in NIST SP 1065 (Table 31, page 108).

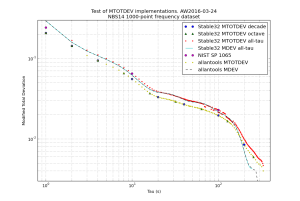
mtotdev_comparison_AW2016-03-24

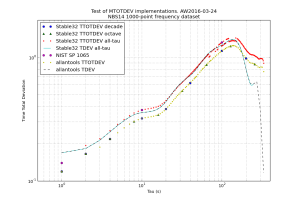
ttotdev_comparison_AW2016-03-24

The figures show mtotdev() and ttotdev() from Stable32 runs and allantools. I've also added mdev() and tdev() traces to compare against. At first sight this looks strange, but mtotdev() is a biased estimator, and Stable32 applies a bias correction which explains the results.

Somewhat surprisingly Stable32 applies a bias-correction only when run in the "all-tau" mode. These numbers agree with those from the NIST SP 1065 table. For this dataset Stable32 is undecided on what power-law the dataset follows at large tau, which results in deviations that jump up and down (because a different bias-correction is applied at different tau, red datapoints).

When Stable32 is run in "octave-tau" or "decade-tau" mode no bias correction is applied. These numbers agree with the ones from allantools.mtotdev().

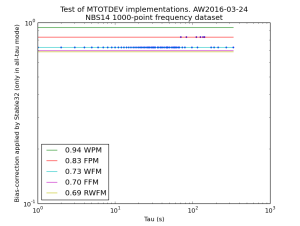
mtotdev_bias_AW2016-03-24

This figure shows the ratio of variances between allantools.mtotdev() (no bias correction) and a Stable32 all-tau run (bias correction applied). The lines correspond to the bias-correction values for different noise processes.

There also seems to be a misprint in NIST SP 1065 equation (28) page 26, where it says ttotdev() is scaled by tau-cubed (when tau-squared is correct). Who reads these things anyway - not many it seems 😉

White Rabbit Workshop, Amsterdam

I gave a talk at the White Rabbit Workshop in Amsterdam about our long link, ideas for fiber asymmetry calibration, and recent stability measurements. The slides are online.

I updated my earlier picture with the noise-floor of three different phase-noise measurement setups. The picture now includes a typical good OCXO trace and the CLK2 10MHz output of a GM-locked White Rabbit Switch (v4.2 firmware).

phase_noise_WR

Symmetricom 6502 distribution amplifier

A look inside the symmetricom 6502 frequency distribution amplifier.

Input stage is based on LMH6702 http://www.ti.com/lit/ds/symlink/lmh6702.pdf.

Output stage is based on LMH6609 http://www.ti.com/lit/ds/symlink/lmh6609.pdf

PDF of sketched schematic, based on the photos: 6502B_schematic_v2

I measured the phase-noise at 10MHz earlier. This amplifier has a far-out phase-noise floor of around -163 dBc/Hz.

Simple Mersenne prime search

For fun I tried to search for Mersenne primes with a very simple code (below). It finds the 20 first Mersenne primes (all known by 1961) in under a minute. After that it slows down quite a lot and finds the 26th prime (discovered in 1979) in about 5 hours.

mersenne_primes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

import time
import math
 
# http://stackoverflow.com/questions/16004407/a-fast-prime-number-sieve-in-python
def prime_sieve(n):
    size = n//2
    sieve = [1]*size
    limit = int(n**0.5)
    for i in range(1,limit):
        if sieve[i]:
            val = 2*i+1
            tmp = ((size-1) - i)//val 
            sieve[i+val::val] = [0]*tmp
    return [2] + [i*2+1 for i, v in enumerate(sieve) if v and i>0]
 
# https://en.wikipedia.org/wiki/Trial_division
def trial_division(n):
    """Return a list of the prime factors for a natural number."""
    if n < 2:
        return []
    prime_factors = []
    for p in prime_sieve(int(n**0.5) + 1):
        if p*p > n: break
        while n % p == 0:
            prime_factors.append(p)
            n //= p
    if n > 1:
        prime_factors.append(n)
    return prime_factors
 
def is_prime_trial_division(n):
    return len(trial_division(n)) == 1
 
# https://en.wikipedia.org/wiki/Lucas%E2%80%93Lehmer_primality_test
def is_prime_lucas_lehmer(p):
    s = 4
    M = pow(2,p) -1
    for n in range(p-2):
        s = (pow(s,2)-2) % M
    return s==0
 
n=2 
t0 = time.time()
print "#\tp\ttime\tyear"
log_max_p=15
for p in range(1,pow(2,log_max_p)):
    if is_prime_trial_division(p):
        if is_prime_lucas_lehmer(p):
            elapsed = time.time() - t0
            print "%4d\t%4d\t%.1f s" % (n, p, elapsed)
            n=n+1