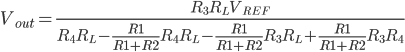I cranked out this 27mm high riser-block from a piece of 35x100 mm aluminium bar today.
The 6mm holes in the corners are for attaching the block to a standard breadboard or optical table that has M6 threads on a 25mm pitch. There are four holes in each corner in a 12.5-by-12.5mm square pattern. These allow attaching the block with 12.5mm 'resolution' both along X and Y.
The middle M6 tapped holes are for attaching to a translation stage. The stage is old with a weird 34x92mm bolt pattern.
A major milestone towards the ion clock was reached today: we trapped the first Strontium ions!
This involves first heating a dispenser that contains Strontium atoms with about 4-5 W (4 A and 1 V). The atoms that fly out of the dispenser are then photoionized using two blue lasers, one at 461 nm and another at 405 nm (we use a laser from a blue-ray drive for this!). We now have Sr+ ions that can be trapped in a Paul trap. A high-voltage (300 Vpp) ~10 MHz sine-wave is applied to the electrodes of the trap. Another blue laser at 422 nm is then used both for laser-cooling and as a means to detect the ion. What we see in the video is the ion fluorescence at 422 nm when it jumps down to the ground state from an excited state. The excited state can also decay into a dark state and we need a re-pump laser at 1092 nm to keep the ion in the Doppler cooling cycle. The fluorescence emitted from one or a few ions is very weak, and we used an image-intensifier and a CCD camera with 500 ms to 1 s exposure time for this video.
The camera software produces FITS frames as output. I used these commands to make the video:
mogrify -format png *.fts # convert to PNG mogrify -crop "640x480+436+315" +repage *.png # crop to the interesting area mogrify -contrast-stretch 10x100 *.png # improve contrast ffmpeg -r 3 -f image2 -i 'myframes_%02d.png' -qscale 1 'video.avi'
On the last line "3" is the desired frame-rate of the output. I then concatenated a few of these videos together with
mencoder video1.avi video2.avi -mf fps=3 -oac copy -of lavf -ovc copy -lavcopts aglobal=1:vglobal=1:coder=0:vcodec=mpeg4:vbitrate=4500 -vf scale=1280:720 -o output2.mp4
This is the same experiment we did back in April, but now "in-situ" in another vacuum system that houses our RF endcap trap. The thin ray of light that slowly switches on and off is a 461nm blue laser-beam that excites Strontium atoms that fly in from the lower right corner of the picture. The on/off switching happens because we slowly scan the laser frequency back and forth and as a result different parts of the atom-stream absorb and emit.
Next stop: ionizing the atoms and trapping a single ion in the RF trap.
See also:
A lot of running along roads, but some orienteering required on controls #5 - #12 also.
On #8 should have followed the straight line via the rocks.
#9-#10-#11 are either on top of a hill or on a steep downslope. It's hard to say how far up or down they are. From #11 I went south and came down the steep and slow slope. Straight west out of the control down a more gentle slope might have been faster.
Then this at #9. Less than 20m from the control I decide it must be more north and do a 4 minute loop.
For pushing a constant 500 uA current through Pt100 temperature sensors I am using a Howland constant current source.
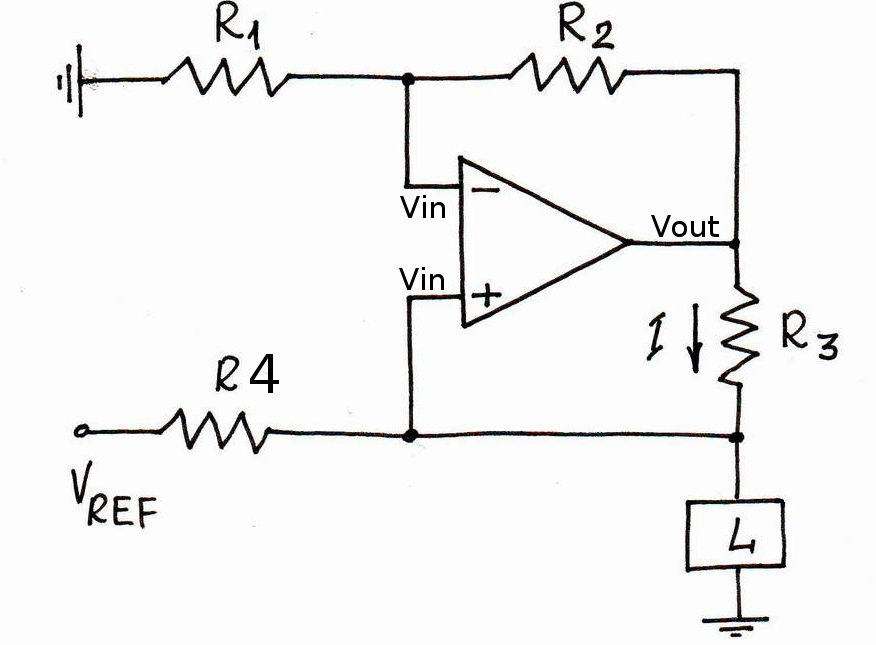
I'm using an OP2177 op-amp. The OPA2188 would have been better, but the delivery time was too long. The four resistors come in a single 4x10k array package, and are matched to within +/-0.05 % (ACASA1002E1002P100). The reference voltage comes either from an external source, or an on-board 5V ADR425.
We did a test of how good the current source is, and came up with this data:
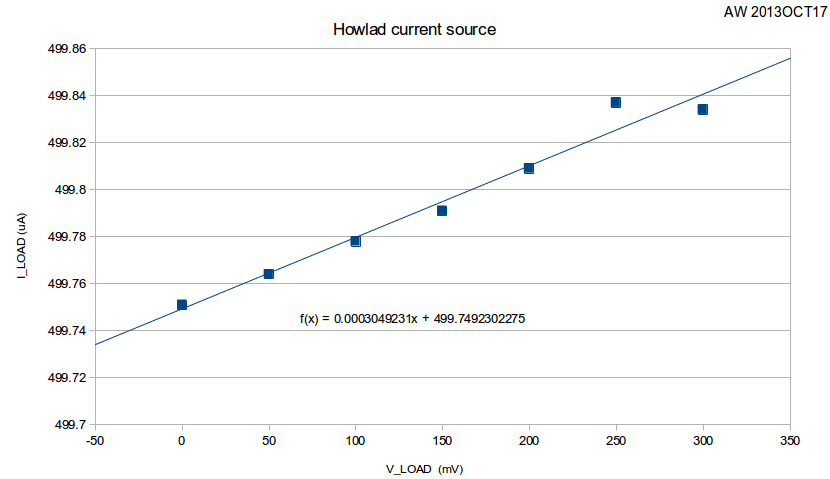
The slope corresponds to an output impedance of 3.6 MOhms. Note that when we change the load resistance from 0 Ohms to 600 Ohms the load current changes by 83 nA, or less than 0.02% of full-scale (500uA). The 6.5-digit multimeter in the electronics lab was mostly oblivious to this change, so we used a 3458A instead 🙂
I then wanted to calculate what contribution the tolerance of the resistors R1-R4 make to the output impedance. Assuming an ideal op-amp (infinite gain, so V+ and V- at same voltage), the op-amp output voltage can be seen to be (left as an exercise for the reader):
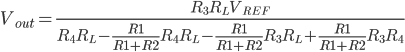
Now we can make a monte-carlo simulation by picking values for R1-R4 with a nominal 10k resistance and an added +/-0.05% tolerance. I did this by adding a normal-distributed resistance with zero mean and 5 Ohm std-deviation.
1 2 3 4 5 6 7 | R0 = 10e3 mu = 0 sigma = (0.05/100)*R0 R1 = R0 + random.gauss(mu, sigma) R2 = R0 + random.gauss(mu, sigma) R3 = R0 + random.gauss(mu, sigma) R4 = R0 + random.gauss(mu, sigma) |
I then repeated the output impedance calculation many times, and plotted this output impedance histogram:
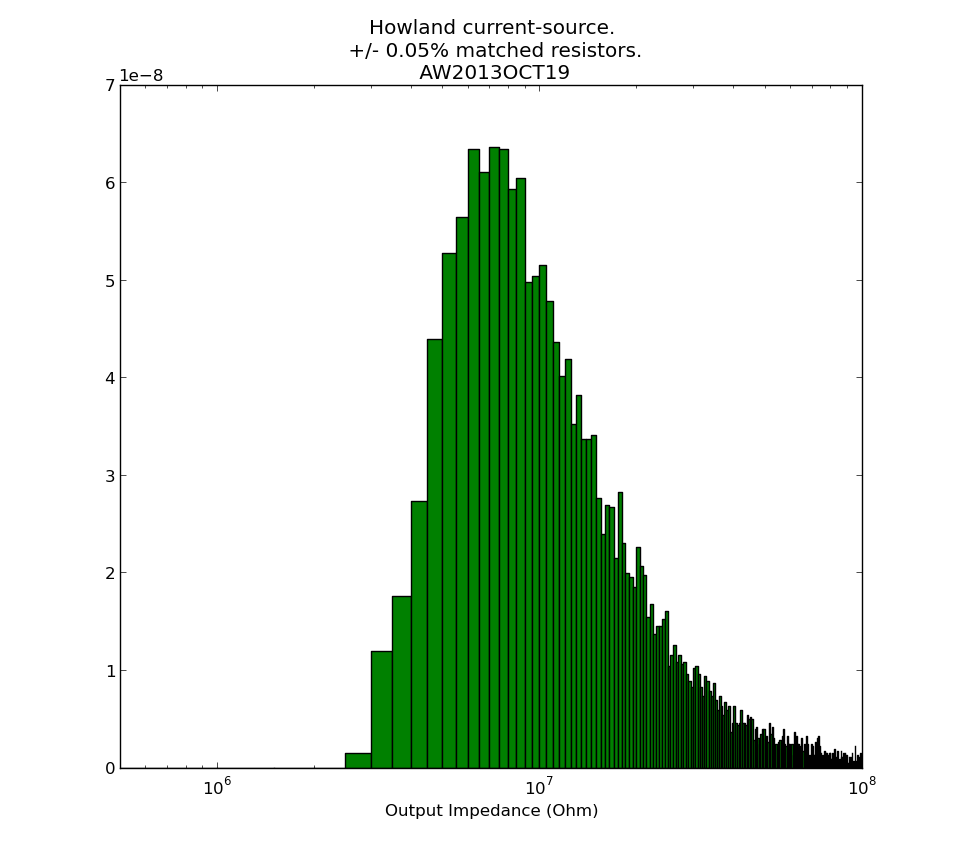
It seems our measured 3.6 MOhms is slightly low, and from the resistors alone something closer to 10 MOhm should be expected. Non-ideal behaviour of the op-amp, which I haven't considered here, may also contribute. Python-script for producing the histogram: howland_calc.py
See also: AN-1515 A Comprehensive Study of the Howland Current Pump (up to 1 MOhm output-impedance with 1% resistors is mentioned)
This current-source is part of the Pt100 frontend.
Reinstalling Ubuntu on my laptop, a Lenovo IdeaPad Yoga 13".
Creating a bootable USB stick:
For some reason the driver support for this laptop is not that great. Wifi, bluetooth, screen brightness control do not work with standard Ubuntu. Amazingly the touch-screen does work - but I don't use it much. The wifi driver is an absolute must, since the machine does not have an Ethernet port.
Wifi driver fix:
git clone https://github.com/lwfinger/rtl8723au.git
cd rtl8723au/
make
sudo make install
sudo modprobe 8723au
Screen brightness fix:
Useful packages and random tweaks:
External sources
sudo apt-get install libappindicator1"NTP to keep the system clock on time
Reasons to still have a Virtualbox Win-7 install:
This was the last of the "iltarastit" events for this year. Next event in April 2014 I guess.
Fast running along paths in Helsinki central park.
Mostly running along paths and roads.
#2 should have chosen the smaller path and a straighter route.
#9 a wrong turn left just at the edge of the control-circle. Should have been easy on compass bearing from the grey cliff.
#13-#14 not great splits, but not that much time lost either.
Night-orienteering yesterday at Kuusijärvi. I managed to be "lost inside the control circle" on four of the ten controls. Being so close to the control and not finding it usually never happens in daylight - but darkness changes everything 🙂
#1: the plan is to use path (A), but I find (B) instead and that works too. North towards the blue swamp with two stones (C), turn right and up onto the grey cliff/hill, and the control should be there. Well no, down the wrong direction of the hill and stop at D. It has to be this hill anyway so I turn back and see some other runners who come out of the control.
#2: On the way to the control hills (A) and (B) are more or less easily recognizable. Then I failed to notice the path between (B) and (C), and didn't see the large stone (C). Aimless circling around until I find the surprisingly large stone (D) (why wasn't it drawn larger?) and ca re-locate roughly on the map.
#5: on compass bearing up the hill A, and then down the steep slope B. Yes! I see the smaller bump C and the control is right behind that one. Eh, well no, maybe it's more north. Meet some other runners at D, turn around, and find the control.
#9: Clearly a difficult control with lots of detail on the map. So a careful start from the very clear corner in the big path A. The plan is to go straight south to the control but the network of paths causes drift to B before my direction turns properly south. Onward south then, but no control in sight and I finally relocate at the highest point on the hill with a steep cliff C. From there finding the control is straightforward.