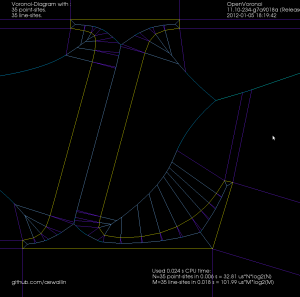
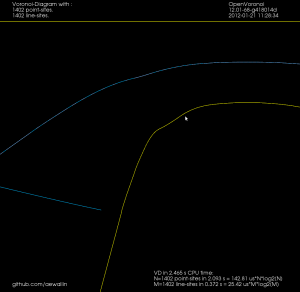
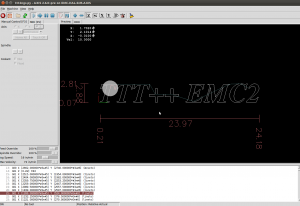
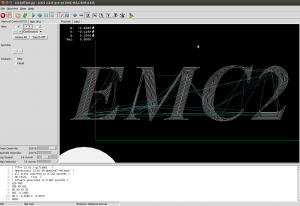
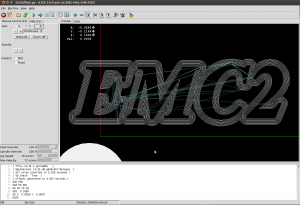
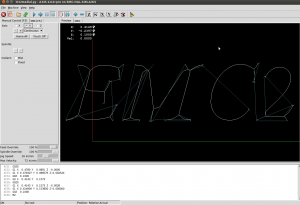
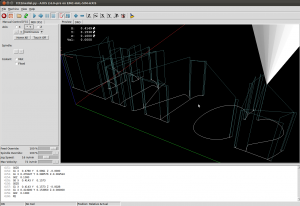
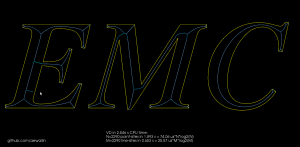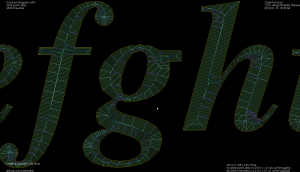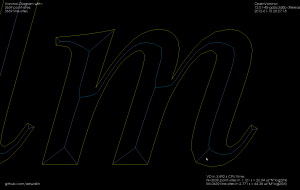A first try at v-carving, with toolpaths produced by the ttt2medial python script.
Non-smooth output from ttt
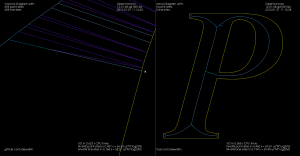
I tried cranking up (10-fold) the number of line-segments that are used when approximating conics and cubics with lines. The results are mostly OK, but sometimes "wiggles" or "S-curves" appear, which cause problems for the medial-axis filter. This "P" is an example:
The medial axis on the right does not look correct. If we zoom in it's clear that there's an "S-curve" in the input geometry, which causes a LINELINE edge (drawn in darker blue), which the medial-axis filter doesn't think should be removed:
For the letters "EMC" it looks mostly OK, but there's a similar wiggle in "E"
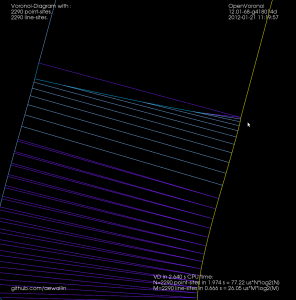
Increasing the number of line-segments further causes even stranger things. Here's a zoom-in at the top of "P" that shows both the wiggle that was visible before, but also a strange inward bulge:
Hopefully this is a bug in how conics/cubics are converted to line-segments in ttt, and not an issue with how FreeType fonts are represented.
EMC2 Filters
I hacked together a few python-scripts that can be run as "filters" in EMC2. They are opened/run from AXIS and produce G-code into EMC2.
The first one is ttt2ngc which simply demonstrates my C++ port of Chris Radek's truetype-tracer. The original code is a rather monolithic C-program while my C++ port is divided into smaller files and offers python-bindings and more options (for example arc, cubic, conic output can be turned on/off independently).
The seconds script is ttt2offset which takes ttt-geometry, builds a VD, and produces offsets. By reversing the list of points from ttt either inwards or outwards offsets can be produced. Currently the toolpaths are machined in the order they are produced, i.e. in order of increasing offset value. An improvement would be to order the loops so that for e.g. pocketing the innermost loop is machined first, and rapid-traverses are minimized.
The third script is ttt2medial. Here the VD is filtered down to an (approximate) medial-axis, and the edges of the medial axis are chained together into a toolpath. The chaining-algorithm could probably be improved much, again to minimize rapid-traverses.
If this is run with a V-shaped cutter with a 90-degree angle we can push the cutter into the material by an amount equal to the clearance-disk radius of the edge. This is a "V-carving" toolpath which should produce a cut-out very similar to the outline of the font. For added effect choose a material with contrasting surface and interior colors.
It would be interesting to know if this v-carving g-code is anywhere near to correct. If someone has a cutting-simulator, or is adventurous enough to run this on an actual machine, I'd be very interested in the results! (here is the g-code: emc2_vcarve.ngc)
Here is a metric version. The max depth is around -3mm, so a 10mm diameter 90-degree V-cutter should be OK. The text should be roughly 100mm long: emc2_vcarve_mm_ver2.ngc
Disclaimer: This is experimental code. Warnings, Errors, and Segfaults are common.
Graph filters
I've put together two graph filters that can be applied to the VD.
The first one detects the interior or exterior of a polygon. When the VD is constructed the polygon boundary must be input in CW order, and any islands inside the polygon in CCW order (or vice versa). This allows running other downstream algorithms only on the parts of the VD that pass the filter. Like these exterior and interior offsets:
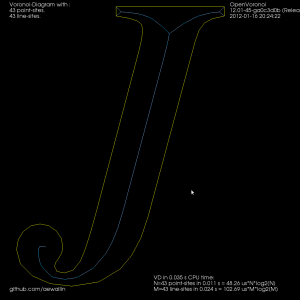
The other filter looks at the interior VD and tries to produce an approximate medial axis. We can start with the complete interior VD, such as this "J":
By definition the medial axis consists of "the set of all points having more than one closest point on the object's boundary". The separator edges shown in purple above can clearly be eliminated, since their adjacent/defining sites are an open line-segment and the segment's endpoint. Removing separators gives us this:
Now we can either finish here, or try to filter out some more edges to make it look better. Since we approximated smooth curves with line-segments we should try to detect which parts of the boundary are really distinct curves, and which are merely many consecutive line-segments approximating a single smooth curve. I've compared the dot-product (angle) between two consecutive segments, and applied an arbitrary threshold:
For the whole alphabet it looks like this.
The choice of threshold value for the angle-filtering is arbitrary. In many cases such as "x" and "m" it results in small or large left-over branches. This could probably be avoided by (1) tuning the angle-threshold, (2) approximating smooth curves with a larger number of line-segments, (3) eliminating branches below a certain length, or (4) choosing a font that's made for v-carving (are there any?).
Although it's probably not right to call it a "medial axis" , the same filter applied to the exterior VD also looks interesting. It divides the plane into organic looking shapes around each letter. It could probably be used for a lot of shape analysis. For example in a smart pocketing routine to find large areas that can be cleared with a large cutter, before a smaller cutter is required for the details. Note that in addition to the geometric shape of all the blue-ish edges the diagram also holds distance-information at each point of an edge. The distance stored is a clearance-disk radius, i.e. we can draw a circle at any point of an edge with this radius, and no input geometry (in yellow) will intersect the circle.
2011 Running/Exercise stats
- 1053 km running. (one marathon, one half-marathon, one 40k march). This is actually slightly down from 1133 km in 2010.
- 2924 km cycling. (five longer trips: 110k 108k 100k 106k+87k)
- 245 km cross-country skiing. (most of it during a week in Äkäslompolo)
- Rogaining: 12h/April and 24h/July
- Orienteering: 7 times (3/June Laakso Pornainen Ilola , 3/July Karjaa Pirttibacka Keimola, 1/October Kerava)
2D Offsets
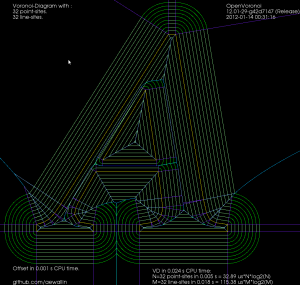
Once we have a VD it is almost trivial to calculate 2D offsets. While the VD for n line-segments takes O(n*log(n)) time to calculate, the offset-generation is a simple "march" that takes O(n) time. In this "A" example it takes 24 milliseconds to calculate the VD and less than 1 millisecond to produce all the shown offsets. Input geometry in yellow, VD in blue. Offset lines in light-green and offset arcs in slightly darker green.
Here is a larger example where VD takes 1.3 seconds, and all offsets shown take 99 milliseconds in total to produce. It would be interesting to benchmark this against libarea or other open-source 2D offset solutions. (here all line/arc offsets in one green color, for simplicity)
Here is a third picture with offsets for a single offset-distance:
GPX-routes with OpenLayers
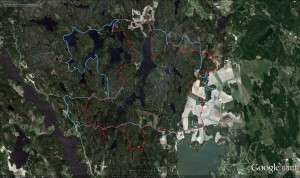
I got a few GPX-tracks from last Friday's rogaining event and drew them with OpenLayers.
Over here: http://www.anderswallin.net/loppiaisrogaining2012/
OpenLayers has a nice set of examples online. Browsing and copy/pasting from examples is much better than trying to read & understand formal documentation.
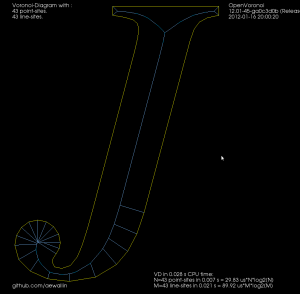
VD Alphabet
There was an issue with handling collinear line-segments, which is hopefully now fixed. OpenVoronoi seems to deal OK with most characters from ttt now.
I am still getting some Warnings about numerical instability from LLLSolver, possibly related to these high-degree vertices which don't look quite right (this is a zoom-in inside the circular dot of "j" in the picture above):

I should write a class for extracting offsets next. Then perhaps medial axis (if anyone is interested in v-carving toolpaths).
8h Rogaining, Espoo
Took part in an 8h rogaining event yesterday. Very wet in the forest with a lot of fallen trees due to the storms over the last few weeks.
We planned a ca. 20km long route (straight lines between controls), assuming we would walk up to 50% more, i.e. around 30km, which would be OK for 8 hours.
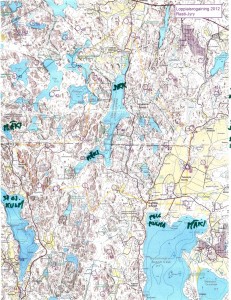
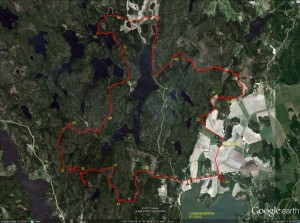
This event had a 1:25000 map which was much easier to read compared to the 1:40000 one last fall. No problems in the beginning, we fould 23 -> 21 -> 31 -> 41 quite easily. The first digit of the control-numnber indicates how many points you get for the control. The next control 51 was worth five points, and they are usually harder to find. Not this time, since it was at the very top of a hill, and people before us had already left tracks in the snow.
Then comes the big mistake of the day. We follow another faster group west down the hill from 51 towards 32. For some inexplicable reason we then completely mis-place ourselves on the map and although we are practically within reach of 32 we make a slow detour south before we realize where we are. Update: I have since learned that our confusion most probably was caused by a brand new road in this area, which was not marked on the map!
Probably annoyed by the first mistake, the second mistake of the day comes on the very next control: between 32 and 37 we take the wrong path north-east and decide to head back when we realize that.
So far we had stuck to the plan, but looking at the watch at 37 we decided to cut 39 from the route. Walk north along the road to 26, and then more walking along a big and then a small road to 57. At 57 we had some discussion about whether to walk back along the road, or try to find the electric lines north of 57 and let them guide us to the road. We had used 4 hours, or half of the total time here. We chose the latter route, and a straight northward pointing bit of our path after 57 indicates where we walked under the electric lines. Close to 53 the plan was to follow a path to the right of the hill and then the ditch to the control. Things didn't go to plan and we ended up to the left of the hill, but found the control with the help of tracks in the snow and voices/lights of others. A walk along the lake-shore to 55. And further north to a road.
So far we had roughly followed the plan. But now we had less than 3 hours left, and it was already dark making orienteering in the woods without clear paths or roads much harder. We decided to forget the plan and walk mostly along roads towards the finish, taking controls close to roads/paths along the way. A long bit of walking first south and then northeast to 49. Another long bit of walking all the way to 24. Here the image shows double GPS-paths because I switched from the 405cx watch to the Edge800 I use on the bike. We still had 45-50 minutes left at 24, so with a close eye on the clock we find 33 quite easily and 22 with a little more effort. We finished with about 12 minutes to spare.
About 90 teams (either solo, or in teams of 2-4 persons) took part.
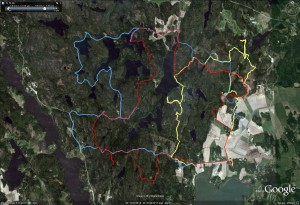
Update, here's our route again (in red), compared to another slightly faster team's route in blue:
TTT++ and font-vd
Update: Now all the capital letters work!

I wanted to test my VD algorithm on font-outlines. So I ported Chris Radek's truetype-tracer to c++ and added some python bindings. Here: https://github.com/aewallin/truetype-tracer
Because my VD code cannot handle circular arcs yet, I took some old code from TTT 3.0 and made converting conics and cubics, the native output of FreeType, as well as arcs into line-segments optional.
Predictably, OpenVoronoi crashes in many cases, but here is an "L" that works: