Lambda exonuclease video
The fourth paper from my thesis, entitled "Dual-trap optical tweezers with real-time force clamp control", has just been published online by Review of Scientific Instruments: http://link.aip.org/link/doi/10.1063/1.3615309
Here's a video from the paper. We are holding on to two micron sized plastic spheres with laser-beams (shown in the video as green/cyan cross-hairs). The lower beam/trap is stationary while the upper one is steerable. A ca 16um long DNA-molecule (invisible) is tethered between the beads.The experiment is performed in the presence of lambda exonuclease, an enzyme that "eats up" one strand of the DNA leaving just a single-stranded DNA-tether between the beads.
In the first part of the video a force-extension curve (bottom panel) is obtained using manual control. We stretch out the molecule by moving the upper trap upwards and check that the force-signal looks like it should when we have a single DNA-molecule of the right length between the beads.
In the second part, after t = 20 s, the tether is held force clamped at 3.4 pN (force shown in top panel). We're keeping the force constant with a PI-controller implemented on an FPGA that reads the force-signal from the lower bead and updates the position of the upper trap at around 200 kHz. As the molecule shortens the controller needs to move the upper trap/bead lower in order to maintain a 3.4 pN tension in the molecule. The video is at normal speed (1X) while the force extension curve is measured. During 13 min of force-clamp control the video is sped up 25-fold. During this time the exonuclease digests one strand of the double-stranded DNA molecule. When held at 3.4 pN of tension, single-stranded DNA is significantly shorter than double-stranded DNA. So the gradual conversion from a double-stranded tether to a single-stranded tether is seen as a decrease in the extension, i.e. a shortening of the distance between the plastic beads (middle panel). The tether broke at t = 880 s. Scale-bar 5 ?m.
Links - 2011 Aug 1
- [Jeri Ellsworth] builds a software radio -
- Frustrating fun with magnetic levitation -
- APOD (Astronomy Picture of the Day) and the Best Astronomy Images -
- Canon EOS 600D Review -
- Canon EOS 1100D Review -
- Why Do You Need 250 60D’s? -
- Building an A Class from Scratch by Mike Connell -
- How to Make a Superlens From Soda Cans -
- Analysis of the Incircle predicate for the Euclidean Voronoi diagram of axes-aligned line segments. (arXiv:1107.5204v1 [cs.CG]) -
- Lets Play Chess -
- Is TJ Tollakson the Graeme Obree of triathlon? -
- All about HeeksCNC post-processing -
- Announcing Git Support for Google Code Project Hosting -
- Space shuttle era ends with Atlantis -
- 2011 Tour de France, Part 2 -
- Google+ -
July macro photos
More playing around with the Sigma 105/2.8 macro lens.
Comparing waterlines
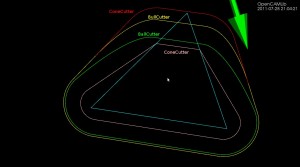
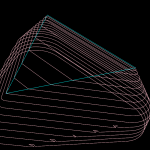
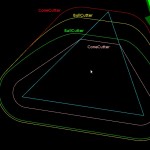
Here's a picture which compares the waterline toolpath for different cutters around a single triangle (cyan). The outermost path (red) is for a cylindrical cutter where we always make contact with either the shaft of the cutter or the circular rim/end of the cutter. Next is the yellow line for the toroidal or BullCutter, followed by the green line for a spherical or BallCutter. The innermost waterline (pink) is for a conical ConeCutter.
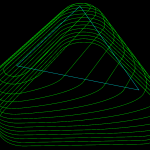
Here are some more waterlines at different heights. This exercise has uncovered at least two new bugs with CylCutter and ConeCutter! The CylCutter seems to fail when asking for a waterline at z=0.0, so that might hint at where the problem is. I'm not sure what is causing the jagged shape with ConeCutter.
Update: The cl-points for conecutter look right, so there must be something strange going on with the weave??
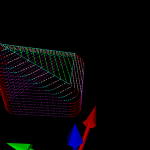
Cone-cutter waterlines
I'm not sure why it has taken so long to get the push-cutter methods for ConeCutter written. You would think that the cylindrical, spherical, or toroidal cases are at least as hard. Somehow I have just avoided working on the cone-cutter...
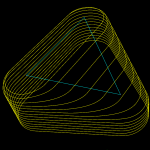
The easy part is as usual contacts between the cutter and the vertices of a triangle - these are shown as red dots. Contact with the facet of the triangle can be made in two ways (1) by the tip of the cone, or (2) by the circular base of the cone, when the facet is steeper than the cone. These are shown in green.
The more involved case is contacts with the edge of the triangle. There are again two cases: We can make contact with the circular base of the cone (cyan dots), or we can make contact with the actual conical part of the cutter (pink dots).
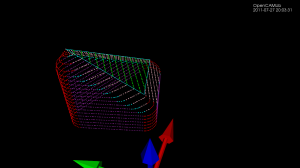
Here is an animation that gives the code a workout. Note how the color of the contact-points changes depending both on what part of the triangle we are making contact with and on what part of the cutter is making the contact.
I have now used github for a while, and will probably merge the conecutter feature-branch into master very soon. Almost as soon as I tried github google-code also started supporting git, but possibly the forking and social aspects of github make a switch worthwhile anyway.
There are some interesting developments on the higher level Waterline/Weave algorithm also, which will reduce the memory-consumption of the algorithm from N*N to N+N (where N is the number of Fibers). This will hopefully make Waterline more useful as now many people have been running out of RAM or just seen sudden crashes. Stay tuned...
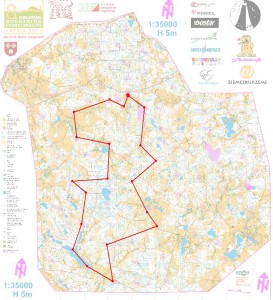
24h Rogaining, Latvia
Update: it seems both persons in our team got infected by Campylobacter from drinking some water from a local well. Lesson: use the water-purification tablets!