40k march

Rounded off a busy week with an organized 40k walk: kesäyön marssi. Walking is obviously not as stressful on the legs and fitness as running, but the script on a 40k walk is pretty much the same: if you are reasonably prepared you will make it until around 25k or 32k without much trouble, and after that it requires some work and determination to finish those last kilometers.

So as not to make it all too easy I cycled 7.3k to work, then 15.5k to the start of the march, and finally 25.9k (at 3am in the morning!) home from the event for a total of ~48k on the bike 🙂

EMC2 tpRunCycle revisited

I started this EMC2 wiki page in 2006 when trying to understand how trajectory control is done in EMC2. Improving the trajectory controller is a topic that comes up on the EMC2 discussion list every now and then. The problem is just that almost nobody actually takes the time and effort to understand how the trajectory planner works and documents it...

A recent post on the dev-list has asked why the math I wrote down in 2006 isn't what's in the code, so here we go:

I will use the same shorthand symbols as used on the wiki page. We are at coordinate P ("progress") we want to get to T ("target") we are currently travelling at vc ("current velocity"), the next velocity suggestion we want to calculate is vs ("suggested velocity), maximum allowed acceleration is am ("max accel") and the move takes tm ("move time") to complete. The cycle-time is ts ("sampling time"). The new addition compared to my 2006 notes is that now the current velocity vc as well as the cycle time ts is taken into account.

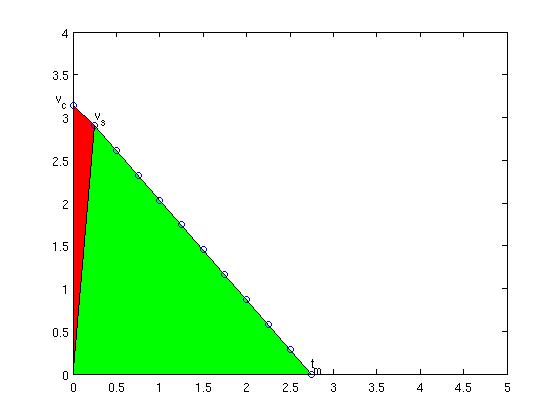
As before, the area under the velocity curve is the distance we will travel, and that needs to be equal to the distance we have left, i.e. (T-P). (now trying new latex-plugin for math:) (EQ1)

Note how the first term is the area of the red triangle and the second therm is the area of the green triangle. Now we want to calculate a new suggested velocity vs so that using the maximum deceleration our move will come to a halt at time tm, so(EQ2):


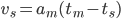
Inserting this into the first equation gives (EQ3):


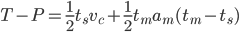
this leads to a quadratic eqation in tm (EQ4):


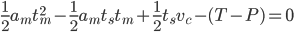
with the solution (we obviously want the plus sign)(EQ5)


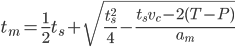
which we can insert back into EQ2 to get (EQ6) (this is the new suggested max velocity. we obviously apply the accel and velocity clamps to this as noted before)


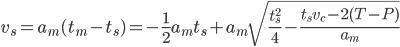
It is left as an (easy) exercise for the reader to show that this is equivalent to the code below (note how those silly programmers save memory by first using the variable discr for a distance with units of length and then on the next line using it for something else which has units of time squared):

discr = 0.5 * tc->cycle_time * tc->currentvel - (tc->target - tc->progress);
discr = 0.25 * pmSq(tc->cycle_time) - 2.0 / tc->maxaccel * discr;
newvel = maxnewvel = -0.5 * tc->maxaccel * tc->cycle_time +tc->maxaccel * pmSqrt(discr);

over and out.

Weave notes

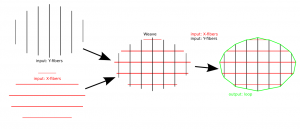
As noted before, the waterline operation consists of radial cutter projection ("push cutter") along fibers/dexels, followed by a weave/grid construction, and contouring to produce the final toolpath. Like so:

The new Weave2 class builds up a half-edge diagram in a smart way, maintaining "next" and "previous" pointers for each edge, so that the green toolpath loop can easily be found by traversing from one CL-point to the next simply following the "next" pointer:


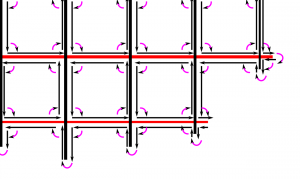
(The magenta arrows are "next" pointers which point from one edge to the next)

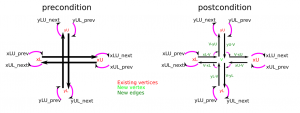
The main part of the algorithm looks at one X-fiber (from xL to xU) and one Y-fiber (from yL to yU) at a time and inserts a new internal vertex (v) into the diagram, while maintaining the existing "next" and "prev" pointers.

I didn't come up with any elegant object-oriented scheme that would do this nicely, so the build() function in the code just peeks and pokes and updates all of the 24 pointers in a brute-force kind of style.

I suspect that the O(n^2) time-complexity is optimal, since with n X-fibers and n Y-fibers there will be roughly n*ninternal vertices in the grid, and they all have to be processed (?unless we can prune the grid and ignore internal areas and focus on the edge of the weave?).

Faster Waterline

I've written a new Weave class for opencamlib which makes the waterline operation faster.

The first test-case is a single triangle, and we calculate a number of waterlines at different z-heights using a ball-cutter:

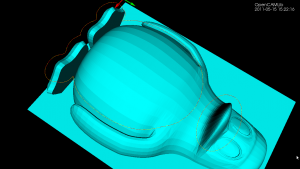
The second test-case is the Tux model where we calculate a single waterline at some z-height. Note how using the chosen ball-cutter at this particular height the waterline splits into two separate loops.

(the yellow line is a plain waterline and the red line is an adaptive Waterline, but that's not important here)

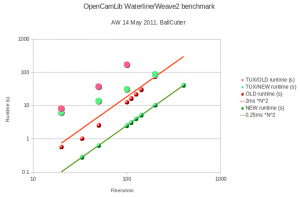
Here is the runtime data. The smaller symbols show results from the one-triangle test-case. The old algorithm(red data points and line) seems to be slower than O(N^2), with a pre-factor of about 2 milliseconds. The time data for the new algorithm (green) fits an O(N^2) line better and has an almost 10-fold faster pre-factor of around 0.25 ms.

The speedup for the Tux model (large symbols) is even greater. With the old algorithm the slope of the data points (pink) looks much worse than N^2 and runtimes quickly reach a minute or more. With the new algorithm (big light green symbols) the runtime stays under 100s even at 200 fibers/mm.

This speedup was achieved by building a weave which is a directed half-edge graph, instead of the old undirected graph. The old algorithm first used connected_components (time complexity O(V + E)) to split the weave into its connected components. For each component a planar embedding was then constructed (time complexity ??), and the toolpath loop extracted with planar_face_traversal (time complexity O(V+E)).

In the new Weave, each edge has a "next" pointer pointing to the next edge of the face. This means we can extract the toolpath loop by following the "next" pointer until we find the next CL-point. Effectively the planar embedding is now contained in the graph datastructure and does not have to be computed separately. This also saves work since we don't have to traverse faces which do not produce toolpaths. This new solution to the weave point-order problemdeserves its own post in the near future - stay tuned...