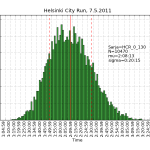
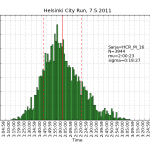
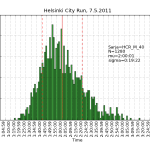
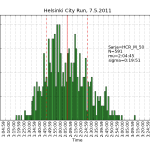
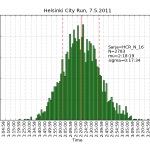
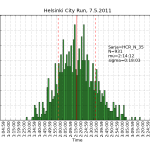
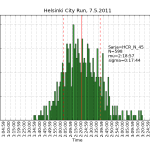
HCR2011 statistics

Using the same scraping scripts I wrote after last years marathon, it was fairly easy to scrape the HCR website and produce some histograms.

There are two python scripts, one that crawls the web (urllib) and finds the time-data (BeautifulSoup and re) and writes to a file (cPickle), and another that reads the files and plots (matplotlib) histograms: hcr2011_scrape

 

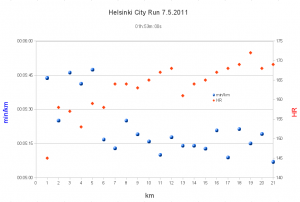
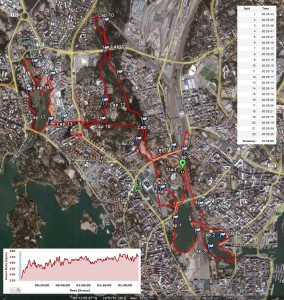
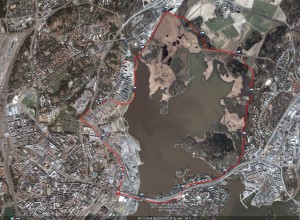
2011 Helsinki City Run

My fourth half-marathon. Not quite a personal best, and my excuse is that the course is a bit up-down hilly and has a lot of turns that slows you down.

Otherwise a solid run with no major problems. A lot warmer than last year, so I ran in shorts and T-shirt. I could put in some work on the uphills which made the HR go >170 and still recover to a reasonable HR 165 or so on the downhills or the flat bits.

My own garmin said 1:53:00, the chip time on the results website seems to be 1:52:57, and the time from the gun was 1:54:14.

The 5k times were: zero to 5k in 28:24, five to 10k in 26:30, ten to 15k in 26:09, fifteen to 20k in 26:25. In other words first 10k in 54:54 and the second 10k in 52:34.

Update: here's the GPS-trace.

TSP

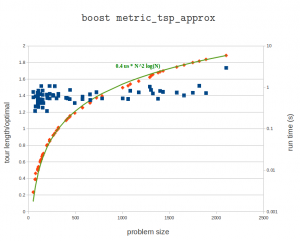
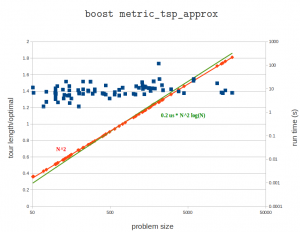
If you have lots and lots of holes to drill on your cnc-machine you might want a TSP solver to optimize the order of the holes so as to minimize rapid movements between holes. I've written a small wrapper around metric_tsp_approx from the boost graph library and included it in opencamlib as a new class TSPSolver. Here's an example on problem "u2152" from TSPLIB95.

Here's a plot of the tour length compared to the known optimal tour length, as well as the run-time on my laptop (P9400 CPU). These problems range in size from 51 points to 2103 points. I might run the bigger problems on the desktop machine later. The algorithm guarantees a tour which is at worst twice the length of the optimal tour. In practice the solutions seem to scatter around 1.4 or 1.5 times the length of the optimal tour. The run times fall neatly on the predicted O(N²*log(N) curve.

A simple greedy heuristic (with better run-time?) which always selects the closest unvisited point also guarantees a tour at most twice the length of the optimal tour.

There's also a better heuristic, the Christofides algorithm, which guarantees a tour length at most 1.5 times the optimal tour length. In addition to the minimum-spanning-tree algorithm it requires a minimum cost perfect matching algorithm. I'm not sure if there is open-source code for this somewhere.

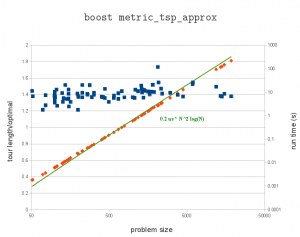
Update: here's a run on an i7-2600K cpu. The pre-factor is now halved to about 0.2 microseconds. The largest problem has 18512 cities and takes over three minutes (217 seconds) to solve.

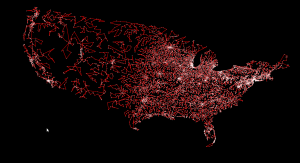
Here's 'usa13509' from TSPLIB. Cities with population at least 500 in the continental US. Presumably from 1995 or so.

 

Scaling (?)

 

Sunday bike ride

First longer ride with the new road bike.

Ride details: 110km, 6h 29min (includes ca 52 min of breaks), avg speed 16.9 km/h, avg HR 123, 2124 kcal.

Bike details: Sabbath September frame with SRAM Rival groupset, 25mm wide 700c Continental tyres. I changed the saddle to a Brooks B17 and fitted a shorter 90mm Easton stem. The saddlebag is a Carradice SQR slim and the bar bag is an Ortlieb classic. Garmin Edge 800 GPS/computer. Shimano A-530 pedals.