Timing build_kdtree()

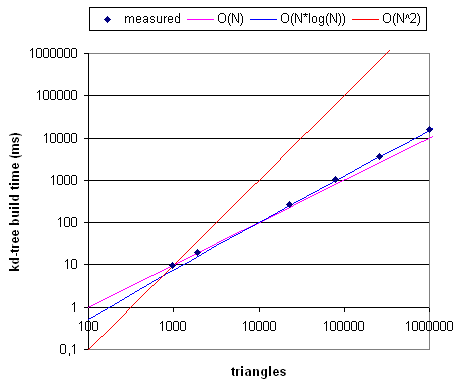
Drop-cutter requires a fast way of searching for triangles under the tool. A kd-tree (4-dimensional in this case) is suggested by Yau et al. I've tried to implement one here (look in trunk/Project2). Just ran some timing tests using Stopwatch() on it, and indeed the build_kdtree() function which takes a pile of triangles as input and generates a kd-tree seems to run in O(N*log(N)) time as it should.

I've never drawn this type of plot before, and I was surprised at how close N*log(N) is to N - in a loglog plot they are almost equal!

This is a recursive function. I wonder if there's a good way of multi-threading recursive functions? My laptop is dual-core and a modern desktop PCs is likely a quad-core - so let's try to write these things multi-threaded from the start.

Next up is a function for doing the orthogonal range-search for triangles that lie under the tool. That's supposed to run in O(N^(1-1/D)+K) time, where D is the dimension of the tree and K is the number of reported triangles - so O(N^(3/4)+K) in this case. I'll try to get that done during the weekend.