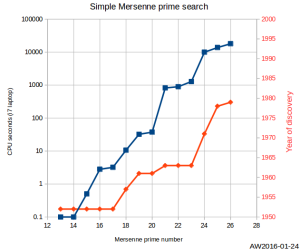
For fun I tried to search for Mersenne primes with a very simple code (below). It finds the 20 first Mersenne primes (all known by 1961) in under a minute. After that it slows down quite a lot and finds the 26th prime (discovered in 1979) in about 5 hours.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | import time import math # http://stackoverflow.com/questions/16004407/a-fast-prime-number-sieve-in-python def prime_sieve(n): size = n//2 sieve = [1]*size limit = int(n**0.5) for i in range(1,limit): if sieve[i]: val = 2*i+1 tmp = ((size-1) - i)//val sieve[i+val::val] = [0]*tmp return [2] + [i*2+1 for i, v in enumerate(sieve) if v and i>0] # https://en.wikipedia.org/wiki/Trial_division def trial_division(n): """Return a list of the prime factors for a natural number.""" if n < 2: return [] prime_factors = [] for p in prime_sieve(int(n**0.5) + 1): if p*p > n: break while n % p == 0: prime_factors.append(p) n //= p if n > 1: prime_factors.append(n) return prime_factors def is_prime_trial_division(n): return len(trial_division(n)) == 1 # https://en.wikipedia.org/wiki/Lucas%E2%80%93Lehmer_primality_test def is_prime_lucas_lehmer(p): s = 4 M = pow(2,p) -1 for n in range(p-2): s = (pow(s,2)-2) % M return s==0 n=2 t0 = time.time() print "#\tp\ttime\tyear" log_max_p=15 for p in range(1,pow(2,log_max_p)): if is_prime_trial_division(p): if is_prime_lucas_lehmer(p): elapsed = time.time() - t0 print "%4d\t%4d\t%.1f s" % (n, p, elapsed) n=n+1 |