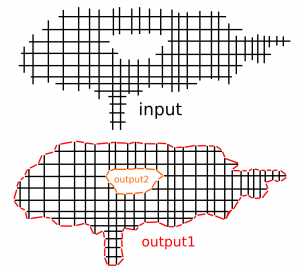
When creating waterlines or 2D offsets using a "sampling" or "CL-point based" approach the result is a grid or weave such as that shown in black above. The black lines can in principle be unevenly spaced, and don't necessarily have to be aligned with the X/Y-axis. The desired output of the operation is shown in red/orage, i.e. a loop around/inside this weave/grid, which connects all the "loose ends" of the graph.
My first approach was to start at any CL-vertex and do a breadth_first_search from there to find the closest neighboring vertices. If there are many candidates equally close you then need to decide where to jump forward, and do the next breadth_first_search. This is not very efficient, since breadth_first_search runs a lot of times (you could stop the search at a depth or 5-6 to make it faster).
The other idea I had was some kind of 'surface tension', or edge removal/relaxation where you would start at an arbitrary point deep inside the black portion of the graph and work your way to the outside as far as possible to find the output. I haven't implemented this so I'm not sure if it will work.
What's the best/fastest way of finding the output? Comments ?!
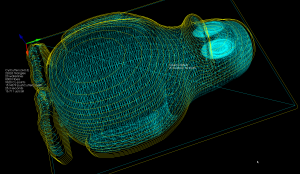
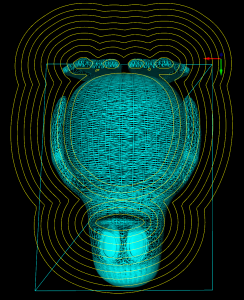
Update: I am now solving this by first creating a planar embedding of the graph and then running planar_face_traversal with a visitor that records in which order the CL-points were visited. The initial results look good:
If you know the xy coords of each vertex then it seems quite stright forward. Is that the case? If not then it's a lot more interesing. I think there's a neat algorithm, that starts with discs on each deg 1 vxt and moves each of them to their adjacent vtx, checks to see if any meet L or R neighbours, then moves discs fwd if there's more than 1 at the vertex, all the time watching out for discs that meet again (just kill then off, but maybe leave a gaurd there). Sorry it's not very clear, just off the top of my head.
Regards, Lou.
the (x,y) coordinates for all the vertices are known (the black lines in the pic). But they are completely unordered, so you don't know between which two vertices to insert the red edges.
in the boost graph-library, theres a Planar Face Traversal algorithm which I will try next.
http://www.boost.org/doc/libs/1_35_0/libs/graph/doc/planar_face_traversal.html