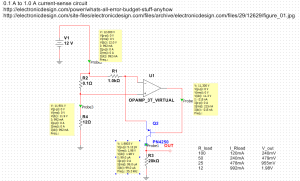
A quick simulation of a current-sense circuit (link via the EEVblog forum)
Author: admin
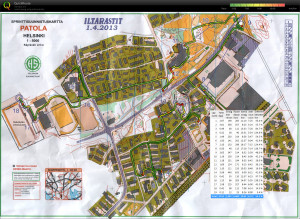
Sprint orienteering, Ågeli
Orienteering again! All of the snow isn't really gone yet, but the orienteering season kicks in anyway.
This was a 3km easy sprint course where the opportunity for making large errors was quite small. In sprint-O keeping out of the prohibited areas (e.g. back-yards, in green on the map) of the map is a challenge - there are lots of DQs for this in competitions.
I'm not sure how bad going off the map is considered. At the top of the map between #9 and #10 there was an open path where I, and everyone else, ran, but according to the GPS-trace it might be just outside the printed map.
TEC mount for laser-module
I made this aluminium bit on the lathe/mill today. It holds a blue laser-module from dealextreme. The brass barrel measured about 11.81 to 11.84 mm in diameter so I first drilled a 10mm hole, then opened it up slowly on the lathe until the module just fit the hole. There is an M3 set-screw to hold the laser module in place. Four long M2.5 screws clamp the aluminium part into contact with a peltier-element and the copper heatsink. A thermistor for temperature measurement and feedback control will be glued to the aluminium part as close as possible to the peltier.
Temperature control of the laser diode should provide for rough tuning of the laser wavelength. We want the wavelength to be about 405.2 nm, to be used for photoionization of Strontium.
Aside: A few years ago I tried to order some of these 405nm laser-pointers to the university. It was impossibly difficult because the shipments were stopped by the customs. Negotiations with the radiation-safety authorities did not help. It's simply forbidden to import non CE-approved laser-pointers - it doesn't matter if you are a researcher or work at a research institution. The story is completely different for laser modules (this is exactly the same product as the laser-pointer, but without the pen-like shape and the battery holder). Apparently these are classified just as "diodes" or "electronic components" and there are no problems getting them through customs.
Noise equivalent temperature in an RTD/Thermistor
How accurately can you in principle measure temperature with an RTD or thermistor?
If we push a current  through the resistor we'll get a voltage of
through the resistor we'll get a voltage of 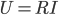 across it. Now as the temperature changes the resistance will change by
across it. Now as the temperature changes the resistance will change by 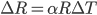 where
where  is the temperature coefficient of the sensor. This will give us a signal
is the temperature coefficient of the sensor. This will give us a signal
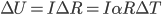
On the other hand the Johnson noise across the resistor will be
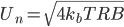 where B is the bandwidth, and we get a signal-to-noise ratio of
where B is the bandwidth, and we get a signal-to-noise ratio of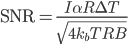
The noise-quivalent-temperature (NET) can be defined as
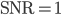 or
or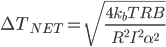
Here we can identify
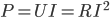 as the power dissipated in the resistor and simplify to
as the power dissipated in the resistor and simplify to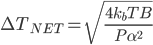
Here's a table with some common values for pt100 and 10k NTC thermistors. The sensitivity  is determined by the sensor type. What limits
is determined by the sensor type. What limits  is self-heating of the sensor which probably should be kept to a few milli-Kelvins in most precision applications. Thermistors with their higher sensitivity are an obvious choice for high-resolution applications, but the lower
is self-heating of the sensor which probably should be kept to a few milli-Kelvins in most precision applications. Thermistors with their higher sensitivity are an obvious choice for high-resolution applications, but the lower  of a pt100 sensor can be compensated with a larger
of a pt100 sensor can be compensated with a larger  since most pt100 sensors are physically larger and thus have lower self-heating. pt100 sensors require 4-wire sensing, slightly more complex than a 2-wire measurement which is OK for a thermistor.
since most pt100 sensors are physically larger and thus have lower self-heating. pt100 sensors require 4-wire sensing, slightly more complex than a 2-wire measurement which is OK for a thermistor.
| Sensor | Resistance | Sensitivity (divide by R to get alpha!) | Dissipated Power P | Noise-Equivalent-Temperature (1Hz bandwidth) |
| pt100 | 100 Ohms | 0.391 Ohms/C | 100 uW (I=1mA) | 3 uK |
| NTC Thermistor | 10 kOhms | -500 Ohms/C | 9 uW (I=30uA) | 0.9 uK |
I conclude that it is not entirely obvious how to choose between a pt100 and a 10k thermistor. The thermistor is intrinsically more sensitive, but with good thermal contact to its surroundings self-heating in a pt100 sensor can be minimized and the same noise-requivalent-temperature achieved. In any case it looks like Johnson noise limits resolution to 1 uK or so in a 1 Hz bandwidth. If we AD-convert the voltage at 24-bit resolution (16M states) we can get a reasonable measurement range of ~32 K by matching 1 LSB = 2 uK.
Does anyone know of similar back-of-the-envelope calculations for other sensors (Thermocouples, AD590)?
Measuring the thermal expansion of ULE glass
Here's an experiment I've done recently:
(Time-lapse of ca 18 hour experiment. Bottom left is a spectrum-analyzer view of the beat-note signal. Top left is a frequency counter reading of the beat-note. Bottom right is a screen showing the a camera-view of the output-beam from the resonator)
This is a measurement of the thermal expansion of a fancy optical resonator made from Corning "Ultra Low Expansion" (ULE) glass. This material has a specified thermal expansion of 0.03 ppm/K around room temperature. This thermal expansion is roughly 800-times smaller than Aluminium, around 400-times smaller than Steel, and 40-times better than Invar - a steel grade specifically designed for low thermal expansion.
Can we do even better? Yes! Because ULE glass has a coefficient of thermal expansion (CTE) that crosses zero. Below a certain temperature it shrinks when heated, and above the zero-crossing temperature it expands when heated (like most materials do). This kind of behavior sounds exotic, but is found is something as common as water! (water is heaviest at around 4 C). If we can use the ULE resonator at or very close to this magic zero-crossing temperature it will be very very insensitive to small temperature fluctuations.
So in the experiment I am changing the temperature of the ULE glass and looking for the temperature where the CTE crosses zero (let's call this temperature T_ZCTE). The effect is fairly small: if we are 1 degree C off from T_ZCTE we would expect the 300 mm long piece of ULE glass to be 200 pm (picometers) longer than at T_ZCTE. That's about the size of a single water-molecule, so this length change isn't exactly something you can go and measure with your digital calipers!
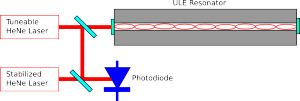
Here's how it's done (this drawing is simplified, but shows the essential parts of the experiment):
We take a tuneable HeNe laser and lock the frequency of the laser to the ULE-cavity. The optical cavity/resonator is formed between mirrors that are bonded to the ends of the piece of ULE glass. We can lock the laser to one of the modes of the cavity, corresponding to a situation where (twice) the length of the cavity is an integer number of wavelenghts. Now as we change the temperature of the ULE-glass the laser will stay locked, and as the glass shrinks/expands the wavelength (or frequency/color) of the laser will change slightly.
Directly measuring the frequency of laser light isn't possible. Instead we take second HeNe laser, which is stabilized to have a fixed frequency, and detect a beat-note between the stabilized laser and the tuneable laser. The beat-note will have a frequency corresponding to the (absolute value of the) difference in frequency between the two lasers. Now measuring a length-change corresponding to the size of a single water-molecule (200 pm) shouldn't be that hard anymore!
Let's say the stabilized laser has a wavelength of 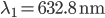 (red light). Its frequency will be
(red light). Its frequency will be 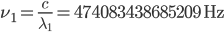 (that's around 474 THz). When the tuneable laser is locked to the cavity we force its wavelength to agree with
(that's around 474 THz). When the tuneable laser is locked to the cavity we force its wavelength to agree with 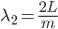 where
where 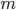 is an integer and
is an integer and 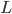 is the length of the cavity. I've drawn only a small number of wavelengths in the figure, but a realistic integer is
is the length of the cavity. I've drawn only a small number of wavelengths in the figure, but a realistic integer is 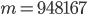 . We get
. We get 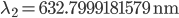 and
and 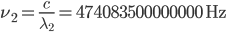 , very nearly but not quite the same wavelength/frequency as the stabilized laser. Now our photodiode which measures the beat-note will measure a frequency of
, very nearly but not quite the same wavelength/frequency as the stabilized laser. Now our photodiode which measures the beat-note will measure a frequency of 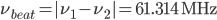 .
.
How does this change when the ULE glass expands by 200 pm? When we heat or cool the cavity by 1 degree C the length changes to 300 mm + 200 pm, and the wavelength of the tuneable laser will change to
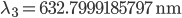 . Now our beat-note detector will show
. Now our beat-note detector will show 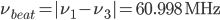 . That's a change in the beat-note of more than 300 kHz - easily measurable!
. That's a change in the beat-note of more than 300 kHz - easily measurable!
That's how you measure a length-change corresponding to the diameter of a water molecule!
Why do this? Some of the best ultra-stable lasers known are made by locking the laser to this kind of ULE-resonator. Narrow linewidth ultra-stable lasers are interesting for a host of atomic physics and other fundamental physics experiments.
See also: Janis Alnis playing with two ultra-stable lasers.
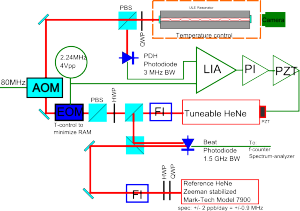
Update 2013 August: I made a drawing in inkscape of the experimental setup.
This figure shows most (if not all?) of the important components of this experiment. The AOM is not strictly required but I found it useful to shift the tuneable HeNe laser by +80 MHz to reach a TEM-00 mode of the ULE resonator. Not shown is a resonance-circuit (LC-tank) between the 2.24MHz sinewave-generator and the EOM. The EOM was temperature controlled by a TEC with an NTC thermistor giving temperature feedback.
Site of the day on EEWeb.com
EEWeb.com will feature this site as the site-of-the-day tomorrow Thursday! Their circuit simulator at www.partsim.com looks interesting:
PD-Amps compared
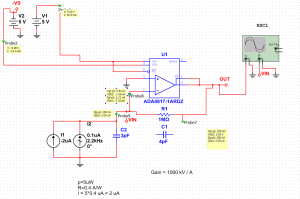
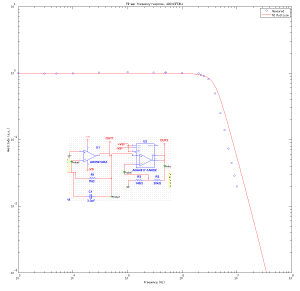
The first design is a single transimpedance-amplifier (TIA) using an ADA4817 and a 1 MOhm resistor. This isn't a great design, since the op-amp is much too fast compared to what is needed/required here. The second design is a 7 kOhm TIA (AD8597) followed by a ~140 V/V gain non-inverting amp (ADA4817). This gives the same total effective gain of ~1 MOhm.
These circuits were designed for a 2 V output with a 2 uA photocurrent produced by about 5 uW of HeNe laser light at 633 nm. The output will hit the "roof" (the positive rail) at about 12 uW of optical power.
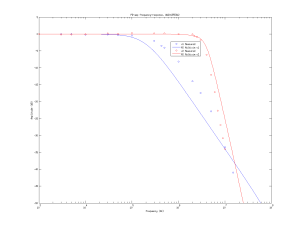
The agreement between simulation and experiment is not very good. I suspect my extremely simple LED-test is to blame. I should build a VCSEL circuit which allows testing these and other photodiode receivers to much higher frequencies.
PD-Amp v.2 assembled and tested
I assembled and tested the latest photodiode-amp today. I tested the frequency response using a red LED driven directly by an Agilent function-generator with an offset of 1.2 V and a 600 mVpp sine-wave. The LED datasheet doesn't specify a rise-time or bandwidth, but I'm hoping it is fast enough to test this 2-3 MHz receiver. I do have some small VCSELs that should be very fast and suitable for testing photodiode receivers up to 500 MHz and beyond.
The signal from the LED caused a 3 V output swing, which explains the slightly lower observed (large-signal) bandwidth compared to the simulated (small-signal) bandwidth. Some of the difference between the simulated frequency-response and the measured one is probably explained by stray capacitance which slightly lowers the bandwidth.
Photodiode amplifier - version 2
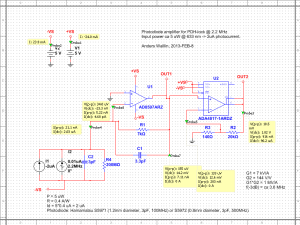
A revised version of the circuit and PCB for a photodiode amplifier, to be used in PDH-locking (Pound-Drever-Hall) as well as RAM-nulling (residual amplitude modulation) in a laser experiment I am doing. The changes compared to the first prototype are:
- The required bandwidth and gain is not easy to achieve in one stage, so there's a second stage of amplification after the transimpedance amplifier.
- I'm suspicious of the noise caused by the switched-mode powersupply, as well as the DC2DC converter, of the previous design. So this circuit has just +/-5 V regulators and can be driven from a regular (known good) +/-12 V lab powersupply (or even two 9 V batteries).
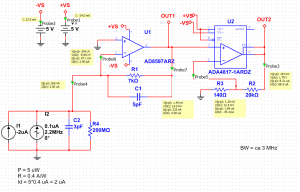
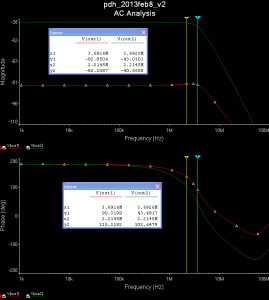
Here is a schematic and simulation results produced with the free version of NI Multisim from Analog Devices. The design is for roughly 1 MOhm of transimpedance gain in total, here split between 7 kV/A transimpedance gain, and 144 V/V for the non-inverting second op-amp. At 1 kV/A of transimpedance gain a 5 uW optical signal at 633 nm (HeNe laser!) that produces a 2 uA photocurrent will result in a 2 V output signal. The AC analysis shows very slight gain-peaking for the transimpedance-stage (red trace) and a -3 dB bandwidth of >3 MHz overall (green trace).
The first op-amp used in the transimpedance stage only needs to have a bandwidth slightly exceeding the transimpedance gain bandwidth (the feedback resistor R1 together with the compensating cap C1, the capacitance of the photodiode C2, and the input-capacitance (not shown) of the op-amp form an RC low-pass filter). The AD8597 is marketed as "ultralow distortion/noise" and is fast enough (10 MHz). The second non-inverting op-amp needs a high gain-bandwidth-product (GBP) since we are amplifying ~100-fold here. The ADA4817 has a small-signal bandwidth of 1 GHz and GBP~400 MHz, so should work OK here.
A voltage of only 14 mV over the transimpedance-resistor is not ideal. The Johnson noise (which in principle a good designer can control/minimize) in the resistor will dominate over the shot noise (which we cannot avoid) in the optical signal. For shot-noise limited performance the rule of thumb is to make the voltage drop at least 51 mV (which will make Johnson and shot noise equal). Without tricks however that is not possible as here we have both a weak signal (2 uA of photocurrent), we want a high gain (1 kV/A in total), and we want to go fast (~3 MHz bandwidth)! If you relax any of those requirements (more power, less gain, slower response) it is straightforward to build a shot-noise limited amplifier in one or two stages.
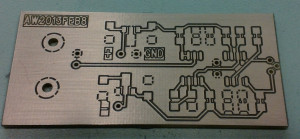
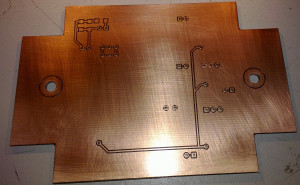
The PCB, fresh from the mill:
Far right is a 3-pin TO-18 socket for the photodiode. Right-middle are the two op-amps with their feedback-resistors/caps, as well as two de-coupling caps for both +5V and -5V. Left-middle are 7805 and 7905 voltage regulators, and the BNC output-connector is far left. All the surface mount components are mounted on the top layer of the board, while the through-hole components are bottom-mounted. Resistors and caps are 1206-size. This PCB should fit the earlier enclosures I turned on the lathe.
Hopefully I will have time to assemble and test one or two of these next week. I should measure the actual frequency-response and compare it with the simulated one.
PI-Controller
I made this PCB on the LPKF mill today:
Moments later, it was populated with components:
This is a PI-controller with three op-amps. One for the P-term, one for the I-term, and one that sums P+I.
The left side of the PCB is a +/-12V power-supply consisting of a DC2DC converter, caps and EMI-filters (Murata NFE61), LM337/LM317 adjustable voltage regulators, and more caps and EMI-filters. Despite the caps and filters I'm not sure this design gives good enough +/- 12V DC supplies for instrumentation use - when the DC2DC input comes from a typical cheap "wall-wart" switch-mode PSU. Or perhaps there is direct RF/capacitive cross-talk from the wall-wart input to the op-amp circuits which shows up as noise in the signal?
The PCB is shaped to fit a Fibox enclosure.