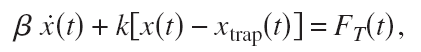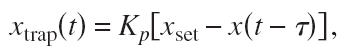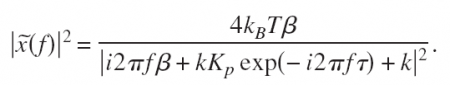Optical Tweezers – Page 2 – anderswallin.net

An optical position clamp

Optical tweezers use light to trap dielectric particles in an approximately harmonic potential. If the position of the bead is X, the position of the trap Xtrap, and the stiffness of the trap k then the equation of motion looks like this:

where Beta is the drag coefficient and Ft is a random white-noise thermal force (the bead is so small that kicks and bumps by surrounding water-molecules matter!). If the trap stays in one place all the time (Xtrap is constant) the power-spectral-density (PSD) of the bead fluctuations turns out to be Lorentzian.

But if there's a fast way of steering the trap, we might try feedback control where we actively steer Xtrap based on some feedback signal:

This is a position-clamp where we use proportional feedback with gain Kp to keep the bead bead at some fixed set-point Xset. Tau accounts for some delay in measuring the bead position and in steering the trap. Inspired by a magnetic-tweezers paper by Gosse et al. we inserted this into the equation of motion to find the PSD:

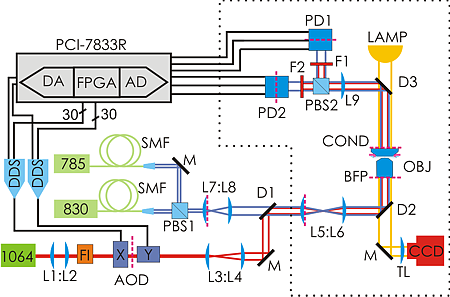
So how do we go about verifying this experimentally? Well, you build something like this:

The idea is to use a powerful laser at 1064 nm for trapping. It can be steered with about a 10 us delay using AODs. Then we use another laser at 830 nm to detect the position of the trapped particle using back-focal-plane interferometry. But since in-loop measurements in feedback loops can give funny results it's best to verify the position measurement with a third laser at 785 nm. The feedback control is performed by a PCI-7833R DAQ card from National Instruments which houses an AD converter for reading in the position signals at 200 kS/s and 16-bit precision, and then we do the feedback algorithm on a 3 Mgate FPGA. We output the steering command as 30 bit numbers in parallel to DDSs that drive the AODs. The 10 us delay in the AOD (the acoustic time-of-flight in the crystal) combined with the AD-conversion time of 5 us gives a total loop-delay of around 15 us in our setup.

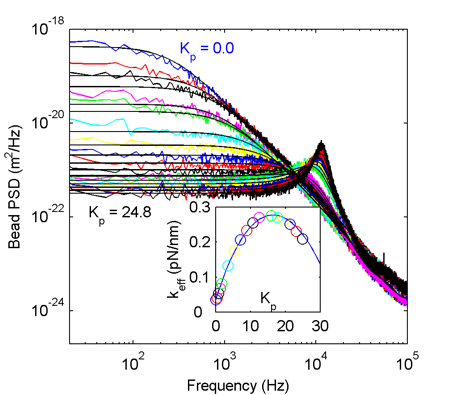
It all works quite nicely! The colored PSD traces are experimental data at increasing feedback gain starting from the blue trace at the top (zero gain, Lorentzian shape as expected) down to the black trace at the bottom (gain 24.8). When increasing the gain further trapping becomes unstable due to the peak at ~12 kHz (think about what's usually termed 'feedback': pointing a microphone at a loudspeaker). The theoretical PSDs are shown as solid lines and they agree pretty well with the experiment. The inset shows the effective trap stiffness calculated from the integral of the PSD. We're able to increase the lateral effective trap stiffness around 10-13 fold compared to the no-feedback situation.

This video shows a time-series of the bead position (left) and the trap position (right) first with no feedback where we see the bead fluctuating a lot and the trap stationary, and then with feedback gain applied (gain=7) where we see the bead-noise significantly reduced and the trap moving around.

These results appear as a 3-page write-up in today's Applied Physics Letters:

A.E. Wallin, H. Ojala, E. Haeggström, and R. Tuma, "Stiffer optical tweezers through real-time feedback control", Applied Physics Letters 92 (22) 224104 (2008) (doi:10.1063/1.2940339)

We're not the first ones to perform this experiment, but I would argue that our paper is the first one to do all steps in the experiment properly, and we get the nice agreement between theory and experiment.

An early paper by Simmons et al. claims a 400-fold improvement in effective trap stiffness using an analog feedback circuit. There's no discussion about the feedback bandwidth or the PSD when position-clamping. Perhaps a case of undersampling?

Simulations by Ranaweera et al. indicate that a 65-fold increase in effective trap stiffness can be achieved, but there's no discussion about how the delays in the feedback loop affect this, and there's no experimental verification.

More recently, Wulff et al. used steering mirrors to do the same thing, but they used the position detection signal from the trapping laser itself for feedback control. I'm not sure what this achieves since the coordinate-system in which you do position measurements is going to be steered around as you try to minimize fluctuations. Their PSDs don't look like ours, and the steering mirror has a bandwidth of only a few hundred Hz so you cannot control the high frequency noise like this.

Increasing the stiffness of optical tweezers by other means seems like a fashionable topic. A recent paper from Alfons van Blaaderen's group uses counter propagating beams to trap high-index (n>2) particles effectively, while simulations by Halina Rubinsztein-Dunlop's group indicate that anti-reflection coating the beads also improves trapping efficiency.

Stretching DNA

Some promising results yesterday with trying to stretch DNA molecules. The molecule is attached between two microspheres, and we are actively moving the smaller sphere while the force acting on the bigger sphere is being measured. The image and video shows the view through a 100x microscope objective on the optical tweezers instrument I am building. Towards the end you can see the construct breaking in two stages, so that probably means there were two molecules of DNA between the beads and not one as intended. This is a control experiment and will hopefully set the stage for bigger and better things to come...

On SNR in single molecule experiments

Wallin, A.E., Salmi, A., Tuma, R. (2007). Step Length Measurement--Theory and Simulation for Tethered Bead Constant-Force Single Molecule Assay. Biophysical Journal, 93(3), 795-805. DOI: 10.1529/biophysj.106.097915

A lot of single molecule experiments are carried out in the configuration shown above. The idea is to mechanically probe a bio-molecule (such as DNA or RNA) or find out how an enzyme (such as RNAP) or a molecular motor (e.g. viral packaging motor) works. You either optically or magnetically trap a microsphere (the round thing with diameter d), which allows you to move it around, measure its position very accurately, and measure the forces acting on the sphere. The sphere is a big thing, usually 500 to 1000 nm in diameter, so it's easily visible in the microscope (the molecules themselves are not visible unless you label them with fluorescent tags).

Then you ask a biochemist in your lab to bind some useful stuff to the sphere. I've illustrated a hypothetical experiment where a molecular motor (MM, grey blob) is bound to the sample chamber wall, and the bead is tethered to the motor via a Worm-Like Chain (WLC, thick wavy line, a common model for polymers such as DNA/RNA).

The problem is that these things are tiny! People want to measure single steps for molecular motors, which can be as short as 0.3 nm. At the same time biological things also live at close to room temperature, so both the molecules and the microsphere are affected by random collisions from the solvent molecules.

Now the question is how small steps or changes in the WLC length are really measurable? It's a bit like going on a walk with your dog: imagine a very flexible string between the dog and yourself. Now if you pull only weakly on the string you can't expect to feel very much of the individual steps the dog takes, you just follow along smoothly while keeping the force approximately constant. If you really want to feel the individual steps you would use a stiffer string and pull much harder on it(but the dog would not like that...). Previous work such as that by Gittes and Schmidt and Moffitt et al. pretty much agrees that the Signal-to-Noise-Ratio (SNR) should look something like this:

where you've used a force to stretch out the WLC (of length L) to an extension xe, the steps you are trying to detect are of size DeltaL, and the stiffness of the WLC is K. In the square root we have gamma (Stokes drag coefficient on the bead), Boltzmann's constant kb, temperature T, and f_lp the measurement bandwidth.

What do we need to do to get a high SNR (and thus measure short steps accurately) ? Use a large force (that increases xe and K), use small beads (that decreases gamma), cool down the lab (decrease T, but not so much so that your biology dies!), and measure slow moving stuff (low f_lp). But this formula is not so practical to use. You need to work out the extension xe yourself and also estimate the stiffness K somehow. I couldn't find anyone who had addressed how this works for common tethers such as DNA and RNA.

My (small) contribution to these thoughts is mainly working out how the SNR really depends on the properties of the WLC and the pulling force. I did a bit of simple theoretical analysis and showed with a Monte-Carlo simulation that the theoretical prediction is about right. This results in SNR 'maps' in parameter space that hopefully can guide experiments. For example if you suspect that your enzyme has a certain step length and you know your tether properties you can use the map or an approximate formula to work out the force you need to have a chance of measuring individual steps.

AOD Steering

I've worked on steering our Optical Tweezers instrument using Acousto Optical Deflectors. Here's an example of what it can do. We're trapping four 1 um silica microspheres in water using a single 1064nm laser that is time shared between the beads (it hops between them at a fast rate). Then we can program the AODs to steer the beads around in whatever patterns we want.