Drop Cutter 3/3: Edge Test

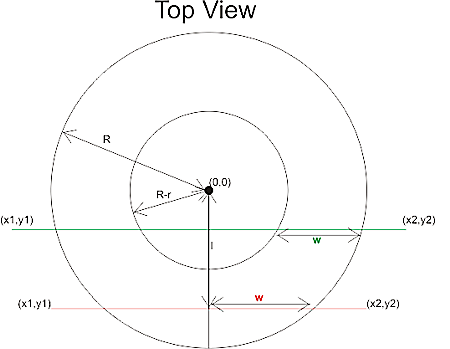
The third and final test in the drop cutter algorithm is to drop the cutter down so it touches an edge. The vertex and facet tests were quite easy, but this one requires a bit of calculations. I'm following Chuang2002.
To simplify things we first translate the tool in the (x, y) plane to (0, 0), and then rotate the edge we are testing against so that it lies along the x-axis and is below the cutter (or on top of the x-axis). The distance from the edge to (0, 0) is l.

Now we imagine a vertical plane through the edge and slice the cutter with that plane. There are two cases, depending on l.

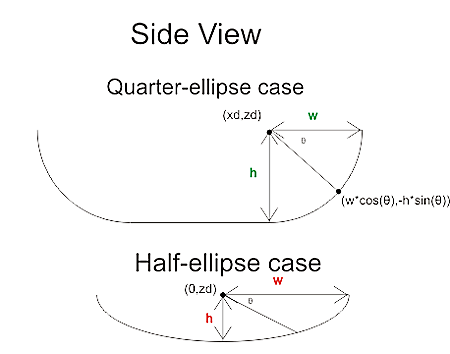
If R-r>l we are cutting with a plane (green) that results in an intersection that has two quarter ellipses at the sides and a flat part in the middle. These ellipses have centers with
xd = +/- sqrt( (R-r)^2 - l^2 )

The other case is shown with a red line: if
R-r<=l<R
the intersection of the cutter will be a half ellipse centered at xd=0.
In both cases the curved part of the intersection is described by
f(theta) = (w*cos(theta) , h*cos(theta) ) where 0<theta<pi
h and w, the height and width of the ellipse are given by

  • quarter-ellipse case:
    • h=r
    • w=sqrt(R^r - l^2) - sqrt( (R-r)^2 - l^2 )
  • half -ellipse case:
    • h=sqrt( r^2 -(l-(R-l))^2 )
    • w=sqrt(R^2-l^2)

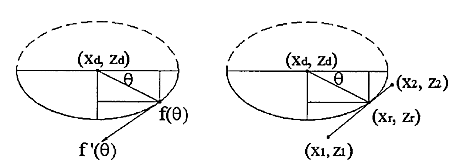
Now that the geometry is clear we can have the edge contact the intersection. That happens at a point where the tangents("slopes") are equal. A tangent vector to the ellipse is given by
f'(theta) = (-w*sin(theta) , -h*cos(theta) )
which can be equated with the slope of the line:
w*sin(theta) / h*cos(theta) = (x1-x2)/(z1-z2)
and we find the angle theta of our CC point:
theta = atan( h*(x1-x2)/w*(z1-z2))
(z1=z2 is a trivial special case not handled here)

The CC point is now given by
xc = xd +/- abs(w*cos(theta))
which should be checked if it lies between x1 and x2. If it does we are contacting the edge, and we can calculate the z-coordinate of the CC point as:
zc = ((xc-x1)/(x2-x1))*(z2-z1) +z1
and finally that leads us to the correct cutter height
ze = zc + abs(h*sin(theta)) - r

Now I need to put all these tests together and find a way of importing STL files into matlab. That way I can begin to test if/how my drop cutter algorithm works!

There's still a lot to do before I have a set of algorithms for basic 3-axis toolpath creation: "push-cutter" a 2D version of drop cutter, 2D line/arc? offsets, zigzag paths, STL-slice with plane, z-buffer simulation of stock material, to name a few things...

Transformer test

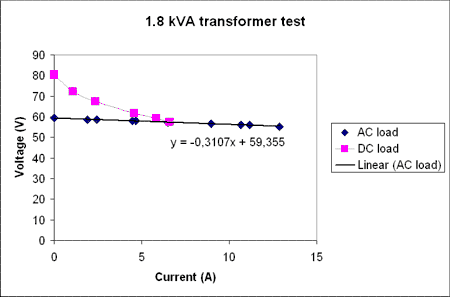
There was something strange going on when I measured the transformer last time, and since that I've gotten a few pointers from visitors to the blog and the CAD_CAM_EDM_DRO list.

I now did a test without the inrush current-limiter, and it does make a difference. It is rated for 8 A continuous current, but apparently it limits current much before that...

Now the 'AC load' line is measured by hooking up resistive loads to the secondary windings (no rectifier or caps), and it shows a series resistance of about 0.3 Ohms, or similar to what can be measured with a multimeter over the secondary windings. So at least the transformer seems to be working.

Then I hook up the secondary to the diode bridge and the caps and connect the same set of resistive loads as before. That's the 'DC load' measurements above. There again I see a big drop in voltage at first that then levels off somewhat. For the points above 5 A current the voltage drop is around 2 V per amp, or about a 2 Ohm effective series resistance. Also, the transformer does not emit any sound at all during the AC test, but now with the rectifier and caps when I load it up there is a slight 'humm' sound(probably 50 Hz and its harmonics).

I wonder if that 2 Ohm is typical or if there still is something strange going on? (could the rectifier bridge be too small? Anything wrong with my 4x 10 000 uF 100 V electrolytic caps?)

I tested this with one bridge rectifier GBPC5004 rated at 400V/50A and another one, a GBPC5010 rated 1000V/50A, but the results are the same. Looking with an oscilloscope at 6 A load at the DC voltage there is about 1.4 V of ripple.

KLV IOM Ranking pictures

Thanks to Jorma Ojama for taking these pictures from the third Finnish IOM ranking event last Saturday.

Olof Ginström was sailing his new FIN-44, the first of three Noux Mk2 designs that will hit the water this summer. The boat worked OK, but the rig still needs some trimming to get up to full speed. I should have my own boat ready in 1-2 weeks.

Opti-BF20 in action

Jari has made an enclosure around our cnc-mill, and that allows us to use a liberal amount of flood coolant. Here's a short video with some tests in aluminium.

Before you run to the shop and get an Opti-BF20 of your own please remember that our machine is seriously modified. We put a new table on it with linear guides, we're using ballscrews, and the stock spindle and spindle motor are replaced.

1800 W 80 V PSU for servos

I've put together a simple unregulated power-supply for use with the DC servos that are going on the cnc-mill in the near future. The design is as simple as it gets: 230 VAC input, fuse, 2-pole switch, inrush-current limiter, 1.8 kVA toroidal transformer with twin 30 V secondaries in series, diode bridge, and finally four 10 000 uF electrolytes.

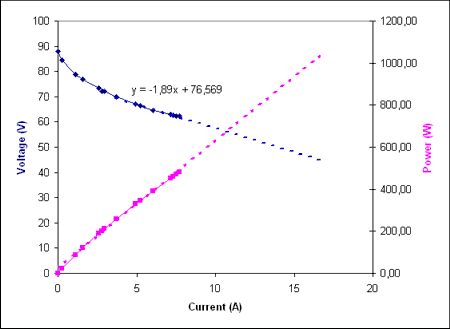
I did a load-test by hooking up various random devices I could find. It didn't exactly go as planned, since most stuff I could find is designed for 230 VAC. I had a resistor rated at 2000 W, a 500 W halogen lamp, a small oven etc. so you would think I could have gotten up to full load? But no, the stuff rated at 230 VAC doesn't dissipate nearly as much energy at 70 VDC 🙁

I was surprised at the largish voltage drop measured, but it's totally unregulated so something like this was to be expected. At about 7 A load I measured a voltage ripple of 1.4 V - which seems OK. A fit to the latter points show an effective series resistance of about 1.9 Ohms for the transformer. I've extrapolated my measurements with dashed lines up to around 1000 W which I estimate is the maximum we will ever use. Hopefully the voltage drop will not be problematic, since overall the system is under closed-loop control.

An emergent spiral

Most conventional CAM algorithms are geometry-based. They create toolpaths that are usually parallel to either the coordinate axes ('zigzag'-paths) or to the part contour (contour-parallel, or spiral paths). One problem with this geometry-based stuff is that you don't take into account the cutting forces. The algorithm has no idea about how much material is removed while the tool is moving. A quick patch is to run a cutting simulation after the path is created and adapt the feedrate for constant material removal rate (MRR).

Another option is to base the toolpath algorithm on a stock model. Then you know the shape of the stock at all times and you can control the MRR or cutter engagement angle. To quickly test how this could work I made a small test in matlab.

The cutter (green circle) is moved around by some rules, and cut's the red pixels as it travels over them. Cut pixels are drawn in blue. The cutter is moved around in discrete steps in some direction, and you're only allowed to cut a certain number of pixels per move. The tricky part is coming up with the rules for our 'lawn-mower' robot. Now I'm using a simple idea: If the past move was made at an angle alfa, try to take the next step in the same direction, but if that's not possible increase alfa until the MRR goes down to some preset value.

This idea will need refinement so that the robot can cope with walls, can do cutting in only one direction (climb vs. conventional) etc. etc., but this seems like a promising and fun start!