Peter Bright from Colombia in South America sent me this picture of his Noux building progress. He's using clay between plywood shadows to build a plug.
Point in triangle test

The facet test I wrote about yesterday needs a 'point in triangle' test to determine if the found CC point lies within the given triangle and we should thus care about the ze value the algorithm determined, or if the CC point is outside, and we can skip to the next test/triangle.
I wrote a function isright(p1,p2,p) which tells me whether the point p is right or left of the line from p1 to p2. The triangle test isinside(p1,p2,p3,p) uses this function three times:
t1 = isright(p1,p2,p);
t2 = isright(p3,p1,p);
t3 = isright(p2,p3,p);
and if t1, t2, t3 all have the same sign then p is inside the triangle.
If I add this function to the facet test, I can determine which of the CC points in the plane containing the triangle are within the triangle:
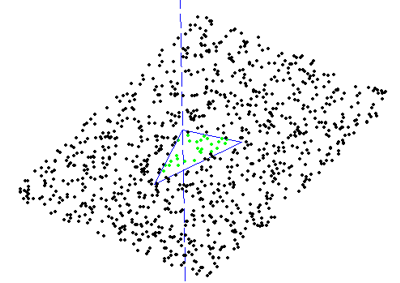
here the dashed line indicates the z-axis.
I'm a little concerned that this works with the projection of the triangle onto the xy-plane. But maybe that isn't a problem because triangles with horizontal normals are special cases anyway. I also haven't yet looked at the rounding/on-edge problems Julian talks about.
I wish the third and final part of this story, the edge-test, was as simple as the vertex and facet tests! At least so far I haven't found a really simple algorithm for the edge-test in the literature (I'm reading Hwang1998 and Chuang2002). Anyone know more about this? please comment below!
Drop Cutter part 2/3: Cutter vs. Facet
Now the problem of contacting a toroidal cutter with the facet of a triangle.
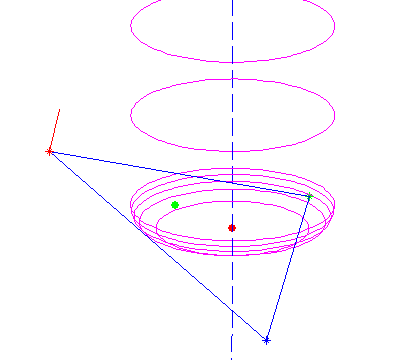
We need to find the equation of the plane which contains the triangle. If the triangle is defined by three points p1 = (x1, y1, z1), p2 = (x2, y2, z2), p3 = (x3, y3, z3) then a surface normal will be perpendicular to both p1-p2 and p1-p3:
N = (NX, NY, NZ) = (p1-p3)x(p1-p2)
and it can be normalized to unit length by setting
n = (nx, ny, nz) = N / sqrt(NX^2 + NY^2 + NZ^2)
I've drawn a surface normal in red in the picture above.
Now the plane containing the triangle is given by
a x + b y + c z + d = 0
where (a, b, c) = (nx, ny, nz) and d can be found by noting that any of the points p1, p2, or p3 must satisfy the equation:
d = - nx*x1 -ny*y1 -nz*z1
the plane is going to make an angle theta with any vertical line, where theta = asin(c)
Then we need a new figure:
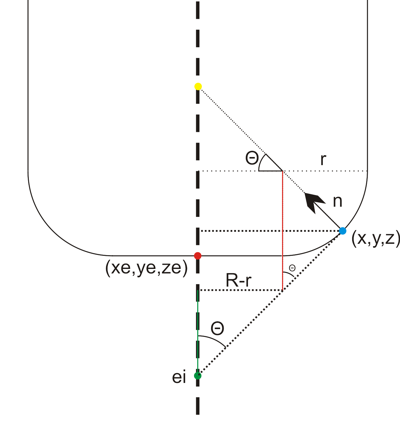
We start out at ei = (xe, ye, zi) , the point on the plane that intersects the line along which we're dropping the cutter (green dot above). It needs to satisfy the equation for the plane, so
zi = - (d + a xe + b ye) / c
Note: c=0 is a special case which needs to be handled separately.
from here we need to climb up to the correct ze, and that's done by first summing the green distance, then the red one, and then dropping down by r:
ze = - (d + a xe + b ye) / c + (R-r)/tan(theta) + r/sin(theta) - r
Now we have the cutter in contact with the plane, but we still need to check that the cutter contact point (CC-point, the blue dot above) is within the triangle facet and not some other point on the plane. To do that we need (x,y,z): If we start at the red point e = (xe, ye, ze) we get to he CC point by travelling upwards to the yellow point, and then along the normal down to the CC point:
CC = e + ( (R-r)*tan(theta)+r )k - ( (R-r)/cos(theta) +r )n
where k=(0, 0, 1) is a unit vector along the positive z-axis.
All of this seems to work as evidenced by the top picture where a toroidal cutter is brought into contact with a facet. The CC point is indicated with a green dot, and the CL (cutter location, or (xe, ye, ze)) point with a red dot.
Now we need to check if the CC point lies within the triangle, but that will have to wait until the next post... (Mr. Todd has some thoughts on this)
Drop Cutter part 1/3: Cutter vs. Vertex
Based on a 2002 paper by Chuang et al., I'm trying to understand the math for calculating 'drop-cutter' toolpaths (Julian Todd also has a lot to say about the drop-cutter approach). The basic idea is that the x,y position of the cutter is known, and it is dropped down along the z-axis until it touches a triangulated surface. A complex surface is built up of many many small triangles, but the algorithm stays the same.
For each triangle there are seven items the cutter might be touching: three vertices, three edges, and one facet (the triangle surface). It looks like a contact point with a vertex is the easiest to calculate, so I'm starting with that. I'm hoping to post part 2/3 and 3/3 of this post soon. They will deal with the facet and the edges.
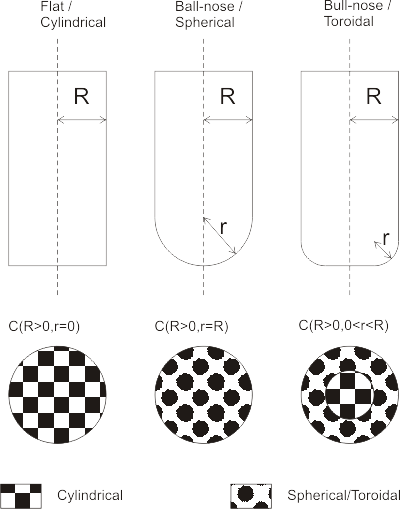
I'm using this fairly simple cutter definition C(R,r) where R denotes the shaft diameter and r the corner radius. The three basic shapes that can be defined this way are shown in the picture. A more elaborate model would include tapered cutters, but I think I won't bother with that now... A cutter thus consists of a cylindrical part or a toroidal part, or both. That means I need six different functions in total for this algorithm:
- Cylinder against vertex
- Toroid against vertex
- Cylinder against facet
- Toroid against facet
- Cylinder against edge
- Toroid against edge
Here's how I think no 1 and 2 work.
Assume the vertex we are testing against is at (x, y, z) and say the cutter is at location xe,ye. We are looking for the cutter z-coordinate ze so at the end when the cutter is in contact with the vertex it will be located at (xe, ye, ze) .
Calculate the distance in the xy-plane from (xe, ye) to (x, y):
q = sqrt( (xe-x)^2 + (ye-y)^2)
Now if q > R the vertex lies outside the cutter and we should report an error or just skip to the next triangle/vertex.
If q <= R-r the vertex lies under the cylindrical part of the cutter and we set ze = z
If (R-r) < q <= R the vertex lies under the spherical/toroidal part of the cutter. This picture should explain the geometry:
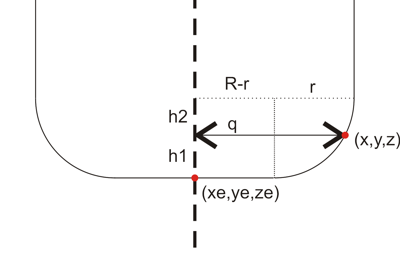
The cutter can be positioned a distance z1 lower than z. To calculate z1 we need z2. It can be found by noting that (x ,y, z) should lie on the toroidal surface:
(q-(R-r))^2 + h2^2 = r^2
or h2 = sqrt( r^2 - (q-(R-r))^2 )
so now h1=r-h2 and we found ze = z-h1
A quick test in matlab seems to confirm that this works:
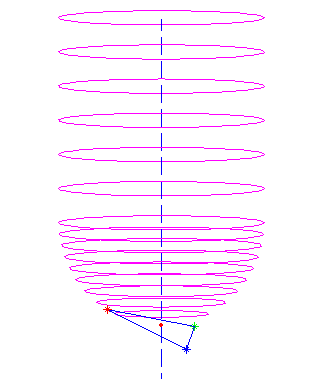
here a ball-nose cutter is dropped down along the dashed line into contact with all three vertices (red, blue, and green stars), and finally it's positioned at the highest ze found (red dot).
Well, that was easy. Now onto the facet and edge tests!
Somewhere... Way up high
One Noux kit for sale
It looks like we will be sailing the first three Noux Mk2 boats early next month. We have a few extra mouldings lying around that are for sale:


This is the glassfiber hull with some wooden planks glued around the edges (for attaching the deck).

Here are the two deck mouldings. The aft deck has a round hole that will fit a Decor lid+rim (the lid Craig Smith uses on his Obsession. One lid+rim is supplied with the kit).

Fin and rudder from carbon fiber.

The kit also contains the fin/mastbox, but it's not attached so you will have to attach it yourself.
These are for sale as a kit. For the hull, the two deck mouldings, fin/mastbox (not attached!), rudder and fin I am asking 400 euros. Buyer pays shipping.
We also have an extra hull, just like the one above, but with no deck or anything additional. If anyone wants it they can have it for 100 euros.
Lead bulbs continue to be available from Olof Ginström for 35euros per bulb. Shipping heavy stuff is expensive, so you could try to meet me at a Nordic Cup event or the Marseille Worlds instead.
Vasa IOM Ranking
Check out the video that Kai Martonen made from this Saturdays IOM event!
Wasa segelförening and iom-nordic should have the results online in a few days.I was sailing a borrowed boat and the lessons are:
(1) water+receiver do not mix!
(2) The mast really needs to stand straight, different-length shrouds are not cool.
A map of Science
A nice map of over 800 000 papers from all areas of science with links indicating citations.
Tiny mobile office?

A friend at work showed me this combination of an N95 and a folding bluetooth keyboard! With 3G/WiFi/GPRS connectivity you can read email and surf the net almost from anywhere. The only thing holding me back is the 690 euro price tag...
Laser methods course in Jyväskylä

I'm in Jyväskylä attending a course on laser measurement methods.


